Transformations: Reflections & Translations

Two common types of transformations Two of the most common types of transformations are translations and reflections. In a translation, something moves from one place to another without changing size or orientation. In a reflection, an image flips to another location, just like with a mirror. Transformations can occur in the coordinate plane. Try this one yourself: Think about seeing yourself reflected in a mirror. How does your hair look the same and different from your real hair? Now picture yourself moving (translating) to another part of the mirror. What changed, and what stayed the same?

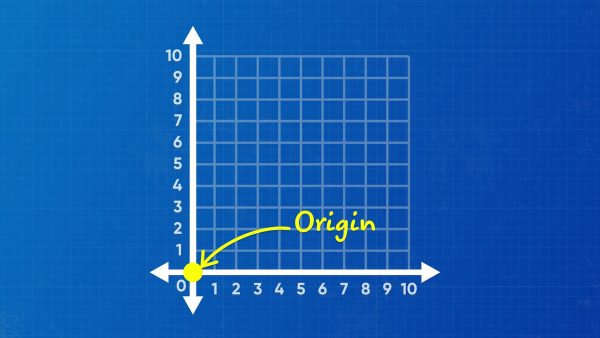
Review plotting points on a coordinate plane The coordinate plane consists of two number lines. The x-axis goes from left to right, and the y-axis goes up and down. The lines meet at the origin, (0, 0). We describe a point on the coordinate plane by its location along these two number lines. The point three units to the right of the origin and five units up is assigned the coordinate pair (3, 5). The point two units to the left of the origin and seven units down is assigned the coordinate pair (–2, –7). Try this one yourself: What coordinate pair represents the point located four units to the right of the origin and six units down?

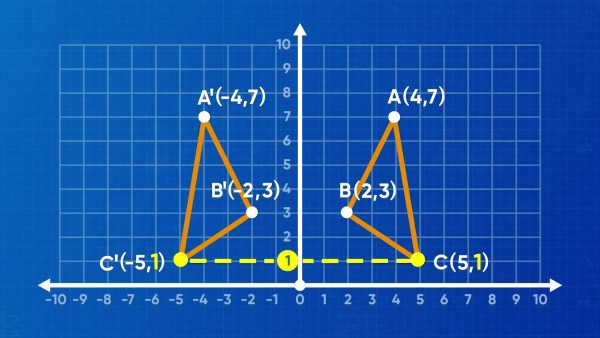
Reflections can create mirror images Design software for a website can be set up like a coordinate grid. Before you reflect a graphic, the graphic is called a “preimage,” like the "pre-transformed image." After you reflect the graphic, the new graphic is called the “image.” When you reflect a pre-image, you have to first choose what line you are going to reflect across, choosing where to put the mirror. To start, you could reflect over the x-axis or the y-axis. When you reflect across the y-axis, the y-values of all of the coordinates stay the same. The x-values are opposite the x-values of the preimage. Just like in a mirror, right becomes left and left becomes right. A triangle with vertices A (4, 7), B (2, 3), and C (5, 1) reflects across the y-axis to A′ (–4, 7), B′ (–2, 3), and C′(–5, 1). The vertices of the image now have ' after their names. A' is read "A prime." Another option is to reflect the pre-image over the x-axis. The x-values of the coordinates stay the same and the y-values become opposite of the y-values of the preimage. In this case, the triangle transforms to A′ (4, –7), B′ (2, –3), and C' (5, –1). Try this one yourself: For a pre-image with vertices at A (0, 0), B (3, 0), C (3, 3), and D (0, 3), what are the coordinates of the image after the pre-image is reflected over the x-axis?

Translations can make an animated superhero fly To make an animated superhero fly across the screen, a visual effects artist must move the image from one place to another. This is an example of a translation. In a translation, the only thing that changes about the pre-image is its location; the angle measurements and side lengths all stay exactly the same. Let’s say a superhero’s head is at (10, 20), and its feet are at (6, 19). If the superhero translates to the right 5 units, only the x-coordinates change. We add 5 to each x-coordinate. The superhero’s head moves to (15, 20), and its feet move to (11, 19). What if, instead of translating to the right, the superhero moved straight down 5 units? In this case, only the y-coordinates change. We subtract 5 from each y-coordinate. The superhero’s head is now at (10, 15) and its feet are at (6, 14). Try this one yourself: A line segment with endpoints at (7, 9) and (5, 11) is translated 4 units to the left. Where are the image’s endpoints?

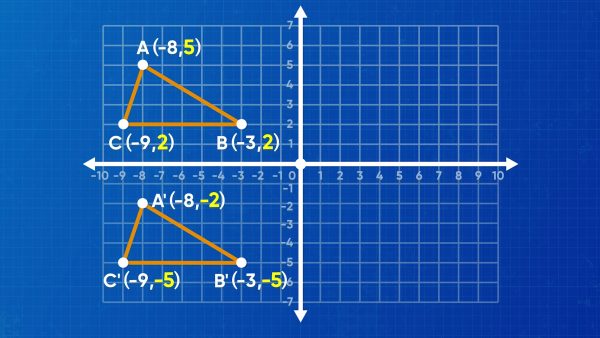
Translations can move in two directions Let’s say a pre-image is a triangle with vertices A (–8, 5), B (–3, 2), and C (–9, 2). A translation three units to the right increases all of the x-coordinates by three, while a translation four units down decreases all of the y-coordinates by four. Vertex A moves from (–8, 5) to become point A′ at (–5, 1). Vertex B moves from (–3, 2) to become point B′ at (0, –2). Vertex C moves from (–9, 2) to become point C′ at (–6, –2).Try this one yourself: If a pre-image is a point located at (6, 1), what coordinate pair represents the image after a translation 8 units left and 3 units up?

A sequence of transformations can reveal congruence Two shapes are congruent when they have the same size and shape. If they are congruent, then you can move one on top of the other for an exact match. That is, the shapes overlap perfectly. Imagine a triangle with vertices F (3, 5), G (3, 2), and H (7, 2). Also imagine a second triangle with vertices J (–1, –5), K (–1, –2), and L (3, –2). Can triangle FGH be transformed onto triangle JKL? In this case, start by reflecting triangle FGH over the x-axis by changing the y-coordinates to their opposites. That gives us points F′ (3, –5), G′ (3, –2), and H′ (7, –2). Then translate this triangle 4 units to the left by subtracting 4 from all x-coordinates. Point F′ moves over to where J is at (–1, –5), point G′ moves over to where K is at (–1, –2), and point H′ moves over to L at (3, –2). There you have it! Since the vertices overlap perfectly, and none of the angles or side lengths changed at all, triangle FGH and triangle JKL are congruent: an exact match! Try this one yourself: Draw two identical triangles in the coordinate plane, where getting to the image requires at least one reflection and one translation. Identify the vertex coordinates of each triangle.