Students learn that division expressions can be written as fractions using the same digits. The numerator represents the wholes being divided and the denominator represents the size of the equal parts.
To better understand Interpreting Fractions as Division…
LET’S BREAK IT DOWN!
Equal Shares – Sandwich, Cakes, and Apples

Let's say that 4 friends would like to equally share 1 sandwich, 2 cakes, and 3 apples. How much of each type of food does each person get? If we cut the whole sandwich into 4 equal parts, which is the same as the division expression 1 ÷4, then each person gets [ggfrac]1/4[/ggfrac] of the sandwich. If we cut each of the 2 whole cakes into 4 slices, which is the same as 2 ÷4, each person gets [ggfrac]1/4[/ggfrac] of the first cake plus [ggfrac]1/4[/ggfrac] of the second cake, or [ggfrac]1/4[/ggfrac] + [ggfrac]1/4[/ggfrac]= [ggfrac]2/4[/ggfrac] of a cake. And if we cut each apple into 4 pieces, which is the same as 3 ÷ 4, and give each person [ggfrac]1/4[/ggfrac] of each of the 4 apples, each gets [ggfrac]1/4[/ggfrac] + [ggfrac]1/4[/ggfrac] + [ggfrac]1/4[/ggfrac] or [ggfrac]3/4[/ggfrac] of an apple. The answers to the division problems tell us the equal amount that each person receives of each food item. Each answer is also a fraction that has the same digits as the division expression. The numerators are the wholes that the friends shared and the denominators show the number of equal parts or equal sharers. We can write division expressions as fractions using the same digits. Try this one yourself: Write a division expression and the answer for the problem: 3 candy bars are shared equally by 5 classmates.
Juice Boxes and Broccoli

Let's say that you have 3 cups of juice to share equally among 5 people. How much juice does each person get? To answer this problem, we write the division expression 3 ÷5, which represents 3 whole cups divided into 5 equal servings. Our answer is a fraction with the number of wholes in the numerator and the number of equal shares in the denominator. Each person gets [ggfrac]3/5[/ggfrac] of a cup of juice. Let's say we would like to equally divide 4 cups of broccoli among 7 people. How many cups of broccoli does each person get? To find the answer, we write the division expression 4 ÷7, which represents 4 whole cups divided into 7 equal servings. Our answer is a fraction with the number of wholes in the numerator and the number of equal shares in the denominator. Each person gets [ggfrac]4/7[/ggfrac] of a cup of broccoli. Try this one yourself: Write a division expression and fraction to represent 9 friends sharing 4 pizzas equal.
Dogs Treats

Let's say you have 24 dog treats for 30 dogs to share equally. Since we have learned that we can write division expressions as fractions using the same digits, we can represent this situation with the expression 24 ÷30. And since we have also learned that the answer to this division problem is the fraction [ggfrac]24/30[/ggfrac], we know that each dog gets [ggfrac]24/30[/ggfrac] of a dog treat. But to measure this out in order to give each dog a treat means cutting each treat up into 30 pieces and giving each dog 24 of those pieces. Since [ggfrac]24/30[/ggfrac] ÷ [ggfrac]6/6[/ggfrac]= [ggfrac]4/5[/ggfrac], we can use the equivalent fraction [ggfrac]4/5[/ggfrac] and say that each dog gets [ggfrac]4/5[/ggfrac] of a treat. Now, let's say the dogs are thirsty and you would like to divide 5 liters of water among the 30 dogs. We can find how much water each dog gets by finding an equivalent fraction for [ggfrac]5/30[/ggfrac], which we solve as [ggfrac]5/30[/ggfrac] ÷ [ggfrac]5/5[/ggfrac]= [ggfrac]1/6[/ggfrac]. Each dog gets [ggfrac]1/6[/ggfrac] of a liter of water, which is the same as [ggfrac]5/30[/ggfrac] liter but makes more sense. Try this one yourself: A farmer would like to divide 7 pounds of chicken feed between 21 chickens. How many pounds of feed does each chicken get?
Bike Ride

You plan to ride your bike 24 miles today, but you would like to break the ride up into 8 equal segments so that you can take breaks between segments. How long is each segment? Since this is an equal sharing problem, we know that we solve it with the division expression 24 ÷8= [ggfrac]24/8[/ggfrac]. Each segment is [ggfrac]24/8[/ggfrac], or 3 miles. Suppose you have 44 liters of water to drink during each of your 8 rest breaks. How much water do you have for each break? We know that 44 liters divided equally among 8 breaks is represented by 44 ÷8, which equals the fraction [ggfrac]44/8[/ggfrac]. We have [ggfrac]44/8[/ggfrac] liters for each break. Another way to solve this problem is to break down 44 liters into 8 groups of 5 full liters (5 × 8 = 40), with 4 liters left to divide among 8 breaks. Our answer using this method is 5 [ggfrac]4/8[/ggfrac] liters of water, which is the same as 5 [ggfrac]1/2[/ggfrac] liters of water, which is also equal to [ggfrac]44/8[/ggfrac] liters of water. Try this one yourself: There are 10 cups of coffee to be shared equally by 4 teachers. How many cups of coffee does each teacher get? Write a division expression and the answer as a fraction or mixed number.
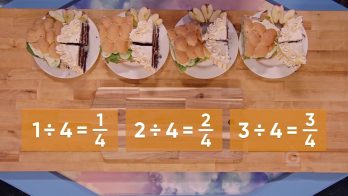
































































































































 Select a Google Form
Select a Google Form






 GENERATION GENIUS
GENERATION GENIUS




