Students are introduced to exponents and powers. They learn how to derive the exponent laws for multiplying and dividing powers, as well as raising a power to a power.
To better understand whole number exponents…
LET’S BREAK IT DOWN!
Powers of 10

If we have 10 × 10, that means we are multiplying by ten two times. We can also express this as 102. 102. We say, “10 to the power of 2.” If we have 10 × 10 × 10 × 10, that’s the same as 104, or “10 to the power of 4.” Now you try: What does 107 mean?
Powers of 2

You get an allowance that starts at $2 a week, and each week, your allowance is doubled! How much allowance do you get on the 20th week? This means that we multiplying 2 twenty times. This huge math equation can be made simpler by expressing it using exponents. 2 multiplied 20 times is the same as 220. That’s equal to $1,048,576! Now you try: How much allowance do you receive on the 11th week?
Multiplying using exponents

The population of rabbits in a town increases rapidly. Last year, the population was 35, and now it is 32 times larger than that! How many rabbits are there now, in all? We can figure this out by multiplying 32 x 35. That is the same as (3×3)×(3×3×3×3×3). Since with multiplication, grouping doesn’t matter, we can rewrite this as 3×3×3×3×3×3×3. That’s 3 multiplied 7 times, which is the same as 37. Notice that 32 x 35 = 37 and 2 + 5 = 7. When we multiply powers that have the same base, we can add the exponents! Now you try: Evaluate 46 x 42.
Powers raised to powers

At the wildlife sanctuary, the population of mice was 24, and the next year, that amount increased to the third power. As a mathematical expression, that looks like (24)3. This means that 2 is multiplied 4 times, and that product is then multiplied 3 times. To understand how to simplify powers raised to powers, we can expand. 24 means 2 × 2 × 2 × 2, so we can also write (2×2×2×2)3. That means (2×2×2×2)×(2×2×2×2)×(2×2×2×2). If we count, we can see that we multiply 2 a total of 12 times. Notice also that 3 × 4 = 12. Then, (24)3 = 212, which is equal to 4,096. When we raise a power to another power, we multiply the exponents together! Now you try: Evaluate (22)5.
Dividing using exponents

A rat family and a hamster family started at the same population. Then the rat family doubled every generation for 3 generations, and the hamster family doubled every generation for 5 generations! How many times larger is the hamster family than the rat family? To solve, we need to represent the hamster and rat populations using exponents, and then divide the hamsters by the rats. Then we have [ggfrac]2⁵/2³[/ggfrac]. We can also express this as [ggfrac]2×2×2×2×2/2×2×2[/ggfrac]. Since any number divided by itself is equal to 1, we can strike out three 2s from the top and three from the bottom. Then all we have left is [ggfrac]2×2/1[/ggfrac], which is equal to 22 = 4. 22=4. The hamster family is 4 times larger than the rat family! When we divide powers that have the same base, we subtract the exponents. Now you try: Evaluate [ggfrac]3⁴/3²[/ggfrac].
Order of operations with exponents
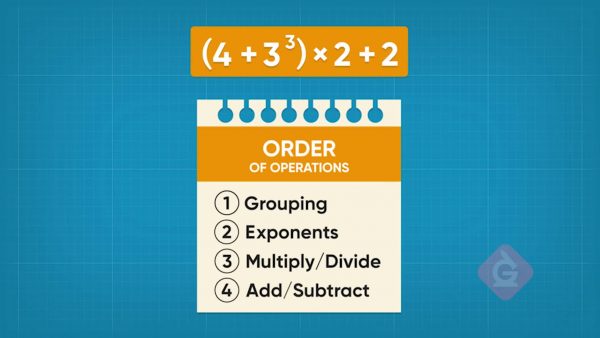
GEMS is a way to remember order of operations. It stands for Groupings, Exponents, Multiply and divide left to right, Subtract and add left to right. Evaluate (4 + 33) x 2 + 2 using GEMS. Groupings go first, so find 4 + 33. 33 = 27, so 4 + 33 = 4 + 27 = 31. Now substitute that into the original expression: 31 x 2 + 2. Multiply next. 31 x 2 = 62. Add last. 62 + 2 = 64. So, (4 + 33) x 2 + 2 = 64. Now you try: Evaluate 99 - (3 x 25).

































































































































 Select a Google Form
Select a Google Form






 GENERATION GENIUS
GENERATION GENIUS




