Volume of Cylinders, Cones & Spheres

Review Volume You can find the volume of a rectangular prism by seeing how many cubic units fit inside it. The number of unit cubes that fit inside tells you the volume. You can also use a formula. The volume of a rectangular prism is length times width times height. If the length is 3 units, the width is 2 units, and the height is 4 units, the volume is 3 × 2 × 4 = 24 cubic units. Try this one yourself: A rectangular prism has length 5 units, width 6 units, and height 2 units. What is the volume of the rectangular prism?

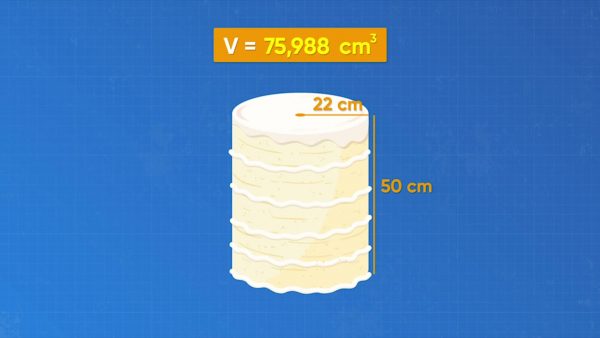
Volume of a Cylinder How can you find the volume of a cake in the shape of a cylinder? Think about this shape by comparing it to a rectangular prism. The formula for the volume of a rectangular prism is length times width times height. The length times the width is the area of the base. So, another way to think of this formula is the area of the base times the height. You can think of the volume of a cylinder in the same way: the area of the base times the height. The base is a circle. A circle has area πr2. So, the formula for the volume of a cylinder is πr2h. Amari’s cake is a cylinder with diameter 44 cm and height 50 cm. What is the volume of the cake? The radius is half the diameter, so the radius is 22 cm. Use the formula. 3.14 × 222 × 50 = 75,988 cubic centimeters. Remember that when you use 3.14 to approximate pi, your answer is an approximation. Try this one yourself: A cylinder has height 20 cm and diameter 16 cm. What is the volume of the cylinder?

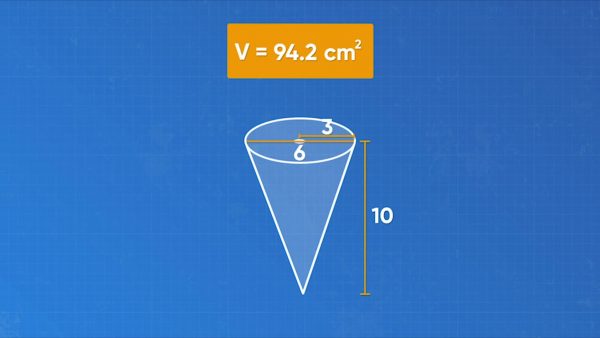
Volume of a Cone How can you find the volume of a plastic cup in the shape of a cone? Compare the cone to a cylinder with the same diameter and same height. If you fill the cone with water and pour it into the cylinder, it takes exactly 3 cones full of water to fill the cylinder. The volume of the cone is one third the volume of the cylinder. Remember, the formula for the volume of a cylinder is πr2h. So, the formula for the volume of a cone is [ggfrac]1/3[/ggfrac]πr2h. Emily has a cone cup. The height is 10 cm and the diameter is 6 cm. What is the volume of the cup? The radius is half the diameter, or 3 cm. Substitute the numbers into the volume formula. The volume of the cone cup is approximately 94.2 cubic centimeters. Try this one yourself: A cone has height 14 cm and diameter 12 cm. What is the volume of the cone?

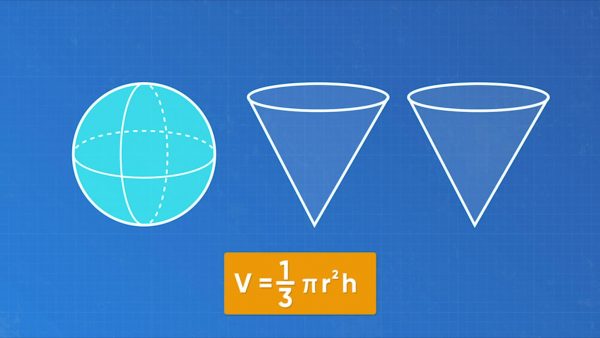
Volume of a Sphere How can you find the volume of a sphere? Compare the sphere to a cone with the same radius and the same height. If you fill the cone with water and pour it into the sphere, it takes exactly 2 cones full of water to fill the sphere. The volume of the sphere is twice the volume of the cone. Remember, the formula for the volume of a cone was [ggfrac]1/3[/ggfrac]πr2h. So, [ggfrac]1/3[/ggfrac]πr2h + [ggfrac]1/3[/ggfrac]πr2h is the volume of a sphere. You can make this formula simpler. The height of the sphere, h, is equal to the diameter, or 2r. Now you have [ggfrac]1/3[/ggfrac]πr2(2r) + [ggfrac]1/3[/ggfrac]πr2(2r). You can simplify this expression. Since you can multiply in any order, move the 2s to the front. Remember, r2 times r is r3. Now you have [ggfrac]2/3[/ggfrac]πr3 + [ggfrac]2/3[/ggfrac]πr3. Add these parts together: [ggfrac]4/3[/ggfrac]πr3. So, the formula for the volume of a sphere in its simplest form is [ggfrac]4/3[/ggfrac]πr3. You could use another version of the formula, but this version is simplest. Use this formula to solve a problem. A fishbowl in the shape of a sphere has diameter 20 cm. What is the volume of the fishbowl? The radius of the fishbowl is half the diameter, so it is 10 cm. Substitute that number into the formula. The volume of the fishbowl is approximately 4,187 cm3 Try this one yourself: A sphere has diameter 18 cm. What is the volume of the sphere?

Relationship Between Cones, Cylinders, and Spheres A restaurant serves smoothies in containers in three different shapes: cones, cylinders, and spheres. All three containers have the same radius and height. All of them are the same price. Which shape container should you order if you want to get the greatest amount of smoothie? Remember, 1 cylinder has the same volume as 3 cones. 1 sphere has the same volume as 2 cones. The cylinder container gives you the greatest amount of smoothie. Try this one yourself: A cylinder and a cone have the same radius. They hold the same amount of water. How many times as tall as the cylinder is the cone?