A system of equations is a set of equations that we need to consider together. A solution to a system of equations is a set of values for the variables that is a solution to every equation in the system.
To better understand systems of equations…
LET’S BREAK IT DOWN!
Make a system of equations to represent BBQ sales.

A system of equations is two or more equations that share the same variables. For example: x + y = 5 and 2x + 3y = 8 are two equations that have the same variables, x and y. They are a system of equations. Here is another example. Adesina bought 1 chicken wing and 1 burger for $8. April bought 6 chicken wings and 2 burgers for $24. How much do each burger and each chicken wing cost? You can write a system of equations to solve. Let c be the cost of one chicken wing and b be the cost of one burger. Then c + b = 8 and 6c + 2b = 24. These two equations form a system of equations that you can solve to find the answer. Try this yourself: You have some dimes and nickels in a jar. There are 8 coins in all. The total value of the coins is 60 cents. Write a system of linear equations to represent the number of dimes and number of nickels in the jar.
Use substitution to solve for the cost of BBQ goods.

You can solve systems of equations using substitution. To do this, rearrange one equation to isolate one variable. Then substitute the value of that variable into the other equation. For the BBQ example, choose either of the two equations to rearrange. Rearranging c+b=8 looks easiest. Pick one variable, and isolate it on one side: b=8-c. Next, replace b with 8-c in the other equation, 6c+2b=24. This gives us 6c+28-c=24. Solve this equation to find the value of c: 6c+16-2c=24, 4c+16=24, 4c=8, and finally c=2. Now we know that a chicken wing costs $2. We can evaluate one of the original equations at that value to find the other cost. It doesn’t matter which equation we use! Using the first equation, c+b=8, substitute c = 2 and solve for b, which is 6. So, we know that a hamburger costs $6 and a chicken wing costs $2. To verify this solution, substitute c = 2 and b = 6 into both equations and check that both sides are equal. Since they are, we know that we have the correct answer. Try this yourself: Solve the system of equations you wrote for the coin problem using substitution.
Solve systems of equations by graphing.
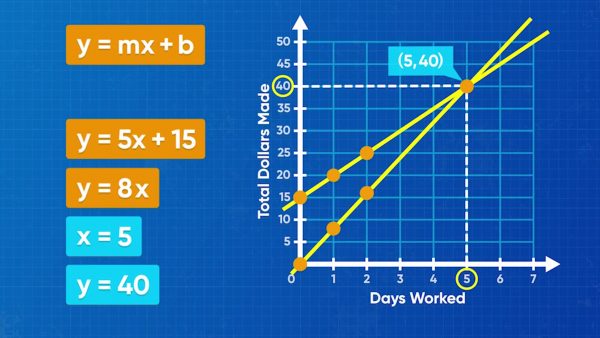
Emily walks dogs, and she makes $8 per day. You can represent the money Emily makes using a linear equation with a slope of 8, y=8x, where x represents the number of days worked, and y represents the amount of money she makes. Amari works at the roller-skating rink. He makes $5 per day, and he already has $15 saved up. You can represent this with the linear equation y=5x+15, where the 5 shows his daily rate, x represents the number of days worked, and the 15 shows how much he has already saved. You want to find how many days they work before Emily and Amari have the same amount of money. Graph both linear equations on the same coordinate plane. Amari's graph passes through the points (0, 15) and (1, 20). Emily's graph goes through the points (0, 0) and (1, 8). The point where the two lines cross is called the point of intersection, and it is the solution to the system of equations. That is because it is the point that makes both equations true at the same time. This point is (5, 40), so on day 5 both Emily and Amari have $40. Try this yourself: Graph the lines y=3x+2 and y=4x-2, mark their point of intersection, and estimate its coordinates.
Many careers require solving systems of equations.

Pilots use systems of equations to determine fuel usage and cost for trips. Wildlife rehabilitation centers use systems of equations to determine the cost of caring for different animals. Chemists use systems of equations to calculate the number of ingredients they need for their reactions. Try this yourself: Can you think of how you can use systems of equations in your life or in a career?

































































































































 Select a Google Form
Select a Google Form






 GENERATION GENIUS
GENERATION GENIUS




