Scientific notation is a shorthand way of writing very big and very small numbers. Scientific notation makes it easier to compare and perform operations on numbers.
To better understand scientific notation…
LET’S BREAK IT DOWN!
You can express huge distances in scientific notation.
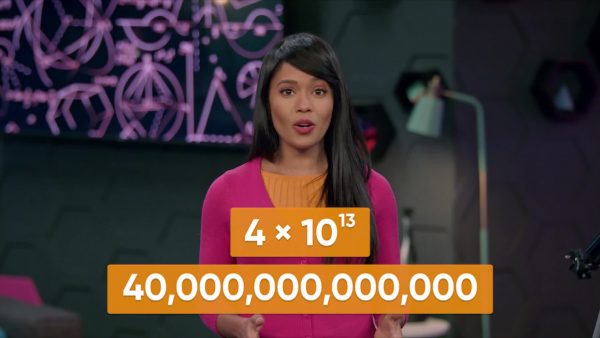
The nearest star to our solar system is Proxima Centauri. It’s about 40 trillion kilometers away. One thousand has 3 zeros, one million has 6 zeros, one billion has 9 zeros, and one trillion has 12 zeros. We can write 4 trillion as 4 followed by 12 zeros. Scientific notation uses powers of 10 to write this more concisely. Scientific notation is written as a number that is at least 1 but less than 10 multiplied by a power of 10. Let's first look at a way to write 40 trillion. 40 trillion is 40 followed by 12 zeros, so 40 trillion = 40 × 1012. This isn't scientific notation because 40 is greater than 10. Take a factor of 10 from 40 and raise the power of 10 to one more power – 1013. 4 x 1013. This is 40 trillion in scientific notation. Try this one yourself: Express the number 18 billion in scientific notation.
Scientific notation uses multiplication and a power of ten.

Suppose a cruise ship goes on a long voyage, covering a distance of 4,000 kilometers. We can rewrite the number 4,000 as 4×1,000. Using tens, the number 1,000 is 10×10×10. Thus, 4,000 in scientific notation is 4 × 103. Another way to find the scientific notation is to consider where the decimal point is in a number. You can think of the number 4,000 as having a decimal point to the right of the last zero. The decimal point needs to move to the right of the 4. Jump 3 place values to the left. The number of places you “jump” to the left is the same as the exponent of the power of 10. Try this one yourself: Express the number 60,000 in scientific notation.
Scientific notation can have more than one non-zero digit.

We can represent the number 64,000 by the expression 64×1,000. Using tens, the number 1,000 is 10×10×10. Remember that in scientific notation, we need a decimal point after the ones place. So, we need to represent 64 as 6.4×10. Thus, 64,000 is (6.4×10)×(10×10×10). In scientific notation, we can represent all 5 of the tens with a single power, so 64,000 is written as 6.4x104. Try this one yourself: Express the number 8,500 in scientific notation.
You can convert numbers in scientific notation to standard form.

The planet Mars is 5.6x107 kilometers away. You can convert this to the standard form by writing out the power of ten: 5.6×10×10×10×10×10×10×10. If you repeatedly multiply 5.6 by 10, it becomes 56, then 560, then 5,600, then 56,000, then 560,000, then 5,600,000, and then 56,000,000. There is a more efficient way to convert to standard form. First look at the exponent. That tells you how many times to shift the decimal point over to the right. In this example, the exponent is 7, so you can write 5.6 and move the decimal point 7 times to the right. Then, write zeros in all the places that are empty. Either way, you get the same value of 56,000,000, or 56 million. Try this one yourself: Represent the distance from the Earth to the Sun, 1.49x108 kilometers, in standard form.
You can express tiny sizes in scientific notation.
An amoeba is a very small creature that you can only see under a microscope. A certain amoeba is 0.0006 meter long. To write this length in scientific notation, you move the decimal point until there is only 1 digit to its left. In this case, move the decimal point 4 times to the right. To write this number in scientific notation, show the number that you have now, which is 6, and multiply it by 10 to the power of negative 4, because you jumped 4 decimal places to the right. Just like the power 104 means to multiply a quantity by ten 4 times, the power 10-4 means to divide a quantity by ten 4 times. In this case, the number 0.0006 is the same as the number 6 divided by 10 to get 0.6, divided by 10 a second time to get 0.06, divided by 10 a third time to get 0.006, and finally divided by 10 a fourth time to get 0.0006 m. Try this one yourself: A bacteria weighs 0.0000052 gram. Express this weight in scientific notation.
You can rewrite numbers in scientific notation with negative exponents in standard form.
A virus Adesina measured was 1.4 × 10-7 meter long. How can you write this length in standard form? 10-7 means divided by 10 seven times, or move the decimal point to the left 7 times. That means that 1.4 × 10-7 = 0.00000014 m. Try this one yourself: A virus has length 7.1 × 10-8. Write the length in standard form.
You can add and subtract numbers in scientific notation.

When two numbers in scientific notation have the same power of 10, add or subtract the numbers that the powers of 10 are multiplied by and keep the same power of 10 in the final sum or difference. You may have to put the sum or difference back in scientific notation. For example, add 8.8 × 103 + 8.6 × 103. Add 8.8 + 8.6 = 17.4. Keep the same power. The sum is 17.4 × 103. The sum is not in scientific notation anymore, so move the decimal point 1 place left and update the exponent: 1.74 × 104. What if the exponents are different? You must make the powers of 10 equal to each other by making sure they have the same exponent. Then you can add or subtract the numbers that the powers of 10 are multiplied by and keep the same power of 10 in the final sum or difference. To add 1.3 × 109 + 6.7 × 107, modify 1.3 × 109 to give it an exponent of 7. So, take 102, or 100, from 109 and multiply it by 1.3. 1.3 × 100 = 130. Now you can add: 130 × 107 + 6.7 × 107 = 136.7 × 107 = 1.367 × 109. To subtract numbers in scientific notation, you can use the same process. Try this one yourself: Subtract 7.1 × 104 - 6.5 × 103.
You can multiply and divide numbers in scientific notation.

Even when their powers of ten are different, you can multiply and divide numbers in scientific notation. This is because of the commutative property of multiplication. You can multiply the decimals, and then multiply the powers of 10. Remember that when you multiply powers of 10, you add the exponents. For example, (1.27 × 104) × (1.09 × 102) = (1.27 × 1.09) × (104 × 102) = 1.3843 × 106. To divide, the process is the same but you subtract the exponents since it’s division: (6×105)÷ (3 × 102) = (6 ÷3)×(105÷ 102) = 2 × 103. Try this one yourself: Multiply(7.1×104) × (6.5×103).

































































































































 Select a Google Form
Select a Google Form








