Scale Drawings (Using Scale Factor)

Use scale factors to make proportional shapes. Computer programs let you make a shape bigger or smaller by dragging an edge or corner of the shape. If you drag the top or bottom edge, the shape gets taller or shorter. If you drag the left or right edge, the image becomes wider or narrower. But when you drag the shape from a corner, the shape can grow or shrink in proportion, meaning it stays the same shape. That’s the idea behind a scale drawing. A scale drawing can be useful because it doesn’t distort a picture when it changes the picture’s size. A rectangular poster designed on a computer might look like it’s 6 inches wide and 8 inches tall on the computer screen. When it gets printed, it could be 5 times bigger by using a scale factor of 5. That means the actual poster is 6×5=30 inches wide and 8×5=40 inches tall. The printed poster and the image on the screen look the same, but the printer posted is bigger. Try this one yourself: On a computer screen, a triangle has base 5 inches and height 10 inches. If you use a scale factor of 3 to print it, what are the dimensions of the printed triangle?

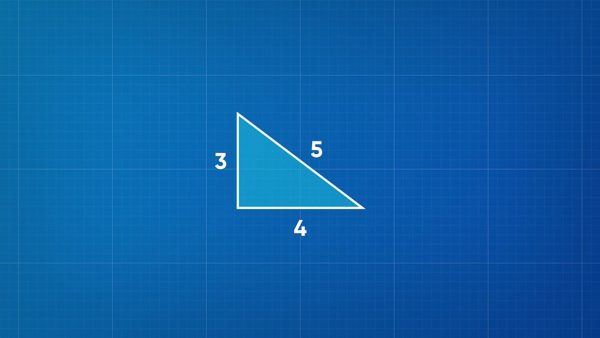
Scale factors can be greater or less than one. The side lengths of a right triangle are 3, 4, and 5 centimeters. To scale it up to a larger image, use a scale factor that’s greater than 1. For example, a scale factor of 5 makes the sides 3×5=15, 4×5=20, and 5×5=25 centimeters long. To scale the original triangle down, use a scale factor between 0 and 1. To make the side lengths half their original size, scale by a factor of [ggfrac]1/2[/ggfrac]. This results in sides that are 3×[ggfrac]1/2[/ggfrac]=1.5, 4×[ggfrac]1/2[/ggfrac]=2, and 5×[ggfrac]1/2[/ggfrac]=2.5 centimeters long. Try this one yourself: A large, rectangular map has base 1 meter and height 2.4 meters. To make a smaller map that is proportional to the first one, the scale factor is [ggfrac]1/3[/ggfrac]. What are the dimensions of the new map?

You can use reciprocals to scale in the opposite way. An artist working for an auto company makes scale models out of clay. The clay model has length 1 meter and the real-life car has length 4 meters. The scale factor from the model to the real car is 4. If the model's height is 0.375 meter, then the real car must have height 0.375×4=1.5 meters. You can also start with a measurement of the real car and scale down by a factor of [ggfrac]1/4[/ggfrac] to find the measurement in the model. A different model shows a 3.5-meter-long car as 0.5 meter long. The scale factor from real to model is 0.5÷3.5=[ggfrac]1/2[/ggfrac]÷[ggfrac]7/2[/ggfrac]=[ggfrac]1/7[/ggfrac]. That means if the height of the real car is 1.4 meters, the height of the model must be 1.4×[ggfrac]1/7[/ggfrac]=[ggfrac]14/10[/ggfrac]x[ggfrac]1/7[/ggfrac]=[ggfrac]2/10[/ggfrac], or 0.2 meter. Try this one yourself: A model car measures 8 cm long and 2 cm tall. The real car measures 400 cm long and 100 cm tall. What is the scale factor from the model to the car? What is the scale factor from the car to the model?

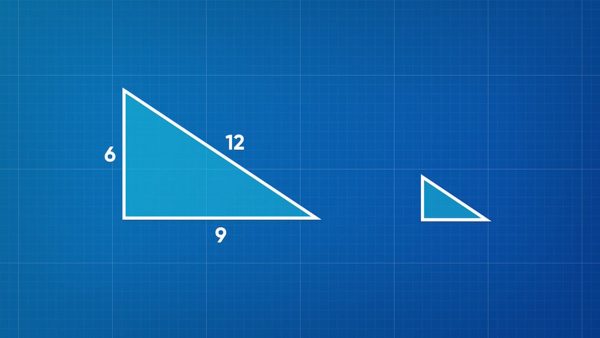
You can use scale factors to solve problems. A triangle has side lengths 6 cm, 9 cm, and 12 cm. These sides are scaled down to make a second triangle where the sides are 2 cm, unknown, and 4 cm, respectively. What is the length of the unknown side? The sides must be scaled by the same factor. Notice that 6 x[ggfrac]1/3[/ggfrac]=2 and 12 x[ggfrac]1/3[/ggfrac]=4. That means the scale factor is [ggfrac]1/3[/ggfrac] from the larger triangle to the smaller triangle. The third side of the smaller triangle must be 9 x[ggfrac]1/3[/ggfrac]=3cm. Try this one yourself: A triangle has side lengths 5 cm, 12 cm, and 13 cm. A second triangle is scaled down from the first, and two of its sides measure 2.5 cm and 6 cm. What scale factor is used to make the smaller shape? How long is the third side of the smaller triangle?

You can make scale drawings on a coordinate grid. You can also make a scale drawing on a coordinate grid. Consider a rectangle that has vertices at A(1, 1), B(4, 1), C(4, 3), and D(1, 3). This rectangle is 3 units long and 2 units tall. A scale factor of 3 makes a larger rectangle by multiplying each side length of the rectangle by 3. The larger rectangle is 3×3=9 units long and 2×3=6 units tall. The coordinates of the larger rectangle could be A'(1, 1), B'(10, 1), C'(10, 7), and D'(1, 7). On the other hand, a scale factor of [ggfrac]1/4[/ggfrac] makes a smaller rectangle by multiplying each side length of the rectangle by [ggfrac]1/4[/ggfrac]. The smaller rectangle is 3x[ggfrac]1/4[/ggfrac]=[ggfrac]3/4[/ggfrac] unit long and 2x[ggfrac]1/4[/ggfrac]=[ggfrac]1/2[/ggfrac] unit tall. The coordinates of the smaller rectangle could be A''(1, 1), B''(1[ggfrac]3/4[/ggfrac], 1), C''(1[ggfrac]3/4[/ggfrac], 1[ggfrac]1/2[/ggfrac]). Try this one yourself: A triangle has vertices at D(5, 0), O(0, 0), and G(0, 10). With a scale factor of 2, where could the vertices D', O', and G' be located? With a scale factor of [ggfrac]1/5[/ggfrac], where could the vertices D'', O'', and G'' be located?

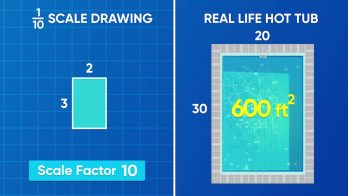
You can use a scale factor to find the area of a shape. Sometimes when people use scale drawings, they tell you the scale using a ratio. Imagine a 1 to 20 scale drawing for the floor plan of a house. This ratio tells how much smaller the drawing is than the real house. When the ratio is written as a scale factor to make the drawing, it may be shown in the form 1:20 or as the fraction [ggfrac]1/20[/ggfrac]. Let’s say a building is 60 feet tall and 40 feet wide. The area of the building’s front surface is 60×40=2,400 square feet. At the scale of 1:20, a drawing of the building is 60 x [ggfrac]1/20[/ggfrac] = 3 feet tall and 40 x [ggfrac]1/20[/ggfrac] = 2 feet wide. The area of the drawing is 3×2=6 square feet. To find the area of a scale drawing, first use the scale factor to find the new side lengths. Then, multiply the side lengths to find the area. Try this one yourself: A scale drawing of a hot tub has the ratio 1 to 10. The drawing is 6 inches wide and 8 inches tall. What is the area of the real-life hot tub?

There are many careers that use scale drawings. Architects use scale drawings to design skyscrapers. They use scale drawings so their designs can fit on blueprint pages. These drawings are scaled down from the dimensions that the skyscraper will be when they build it. Architects can even use scale drawings to make scale models. This allows them to make sure the design is right. Engineers use scale drawings to design everything from bridges to space shuttles. Space shuttle parts are very expensive to make. Engineers can use scale drawings to make sure every part is the right shape and size for the build before the real parts are created. Fashion designers use scale drawings to make clothes. Everyone’s body is different, so a designer can scale up or scale down their design to fit each client perfectly.