Proportional Relationships

Make muffins using a proportional relationship.

To make 1 dozen muffins, you need 2 eggs. If you want to make 2 dozen muffins, you need 4 eggs. To make 3 dozen muffins, you need 6 eggs. 1 times 2 is 2, 2 times 2 is 4, 3 times 2 is 6. The number of eggs is always 2 times the number of batches of muffins. This is called a proportional relationship. Now you try: How can you tell if the following data represents a proportional relationship? 1:3, 2:6, 3:9, 4:12

The constant of proportionality is the multiplication factor.

Adesina works different numbers of hours at a skating rink. The amount of money she makes for each number of hours she works is represented by this relationship: 1:$5, 2:$10, 3:$15, 4:$20, 5:$25. Is the relationship proportional? 1 times 5 is 5, 2 times 5 is 10, and so on. The number of dollars earned is always 5 times the number of hours worked. The relationship is proportional. The number that you always multiply by is called the constant of proportionality. The constant of proportionality of this relationship is 5. Now you try: What is the constant of proportionality for the following set of ratios? 2:14, 3:21, 4:28, 5:35

You can identify if a relationship is proportional.

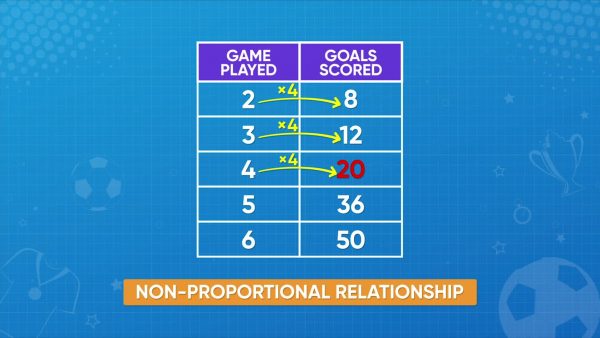
The following data shows the number of soccer games you played related to the number of goals you scored: 2:8, 3:12, 4:20, 5:36, 6:50. 2 times 4 is 8, and 3 times 4 is 12. But 4 times 4 is 16, not 20. And 5 times 4 is 20, not 36. You can't always multiply the number of games played by the same number to get the number of goals scored. This is a non-proportional relationship. Now you try: Identify if the following data represents a proportional relationship: 3:9, 5:15, 6:24, 8:32

You can describe proportional relationships using equations.

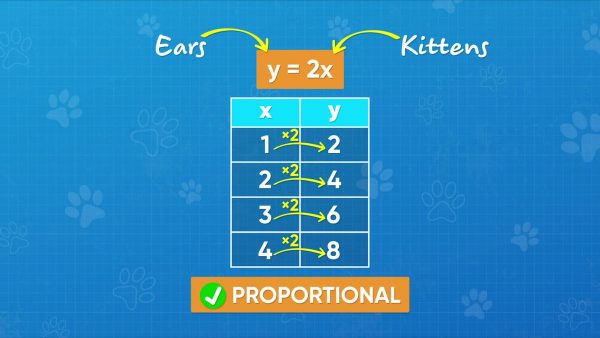
Every kitten has 2 ears. You can write an equation to show how the number of kittens is related to the number of ears. Let x be the number of kittens and y be the number of ears. So, y=2x, since the number of ears is always twice the number of kittens. You can plug in any number of kittens for x to find the number of ears, y. For example, 5 kittens have y = 2 × 5 = 10 ears. Now you try: Write an equation to describe the relationship between the number of dogs and the number of legs in all.

You can recognize proportional relationships in equations and graphs.