Probability tells us how likely it is that something will happen. We can write probability as a percent, a decimal, or a fraction. The lesser the probability, the less likely the event is to occur.
To better understand probability of single events…
LET’S BREAK IT DOWN!
Find the probability of a coin toss.

A football match starts with a coin toss to decide which team starts with the ball. The coin has two sides, heads and tails. What is the likelihood, or the probability, that the coin turns up heads? The coin has two sides, so there are two possible outcomes of the coin toss. There is only one way for the coin to turn up heads. This means that the probability is 1 out of 2, [ggfrac]1/2[/ggfrac], 0.5, or 50%. The probability of tails is the same because there is only one way to come up with tails, out of two possible outcomes. Because the two events, “heads” and “tails,” have the same probability, they are equally likely. Try this yourself: A number cube has 6 sides, labeled 1 to 6. What is the probability of rolling a 1?
Probability tells you the likelihood of events.
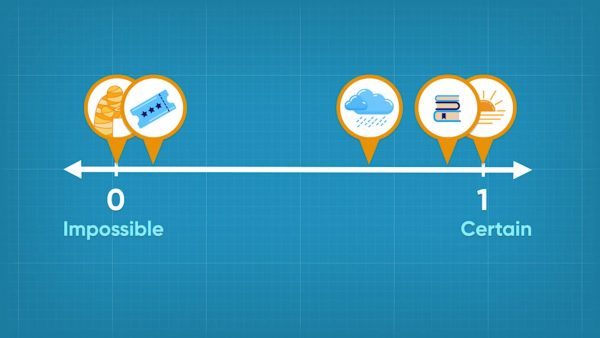
Probabilities range in size from 0 to 1. You can describe how likely events are by their probability. If an event is impossible, it has a probability of 0. If an event is certain, it has a probability of 1. If the event is as likely to happen as it is to not happen, its probability is 0.5. If an event is not likely to happen, but still could happen, like winning the lottery, the probability is close to 0. If an event is very likely to happen but might not happen, like having homework after school today, its probability is close to 1. Try this yourself: On a number line from 0 to 1, with 0 being impossible and 1 being certain, how likely is it that it will rain today? Check the weather forecast: what probability do they give for rain today?
Find the probability of outcomes on a wheel.

A game wheel has 10 equal sections, labeled with numbers 1 to 10. This means there are 10 possible outcomes. There is only one way to spin a 2. This means that the probability of spinning a 2 is 1 out of 10. You can also write this as [ggfrac]1/10[/ggfrac], 0.1, or 10%. What is the probability a spin lands on a number (it doesn't matter which one)? There are 10 ways to spin any number and 10 possible outcomes. The probability of spinning any number is 10 out of 10, [ggfrac]10/10[/ggfrac], 1, or 100%. This means the event “spin any number” is certain. It also makes sense because you land on a number 100% of the time. Try this yourself: If the wheel has 25 equal sections, labeled with numbers 1 to 25, what is the probability of spinning a 7? What is the probability of spinning a number 15 or greater?
The sum of all possible probabilities is 1 or 100%.

On the original game wheel, the probability of spinning a specific number is [ggfrac]1/10[/ggfrac]. The probability of spinning any number at all is 1. The sum of the probabilities of spinning each number is 1. So the probability of spinning any number on the wheel is the same as [ggfrac]1/10[/ggfrac] + [ggfrac]1/10[/ggfrac] +[ggfrac]1/10[/ggfrac] + [ggfrac]1/10[/ggfrac] + [ggfrac]1/10[/ggfrac] + [ggfrac]1/10[/ggfrac] + [ggfrac]1/10[/ggfrac] + [ggfrac]1/10[/ggfrac] + [ggfrac]1/10[/ggfrac] + [ggfrac]1/10[/ggfrac] = [ggfrac]10/10[/ggfrac] = 1. Try this yourself: If the wheel has 25 equal sections, labeled with numbers 1 to 25, what is the probability of spinning any of the 25 numbers on the wheel?
Compare experimental and theoretical probabilities.

You flip a coin 10 times. You expect to get 5 heads and 5 tails, because the probability of the coin landing on each side is [ggfrac]1/2[/ggfrac], or 50%. The result of your flips is 6 heads and 4 tails. Why didn’t you get 5 heads and 5 tails? The probability, 50%, is the theoretical probability. The results of your experiment are a probability of 60% heads and 40% tails. This is the experimental probability. It is the result of an experiment. As you do more and more flips of the coin, the experimental probability will get closer to the theoretical probability. This effect is called the Law of Large Numbers. Try this yourself: If you flip a bottle 100 times, and in 20 of the trials the bottle lands on its base, what is the experimental probability of the bottle landing on its base?

































































































































 Select a Google Form
Select a Google Form








