In probability, compound events are two or more events that happen together. For example, two coins are flipped or one coin is flipped and then flipped a second time.
To better understand compound events…
LET’S BREAK IT DOWN!
Calculate the probability of flipping a coin and getting heads twice.

Let’s say you want to flip a coin twice and calculate the chance of getting heads twice. This is a compound event, since it is two events happening together: two coin flips. First, calculate the probability of getting heads on one coin toss. There are two possible outcomes, heads or tails, and you are looking for one of those outcomes: heads. The probability of getting heads on one coin toss is 12. To find the compound probability, you can list all of the possible outcomes: [H, H], [H, T], [T, H], [T, T]. There are 4 possible outcomes. Only one of the outcomes is 2 heads. The probability of getting heads twice is 14 or 25%. Try this one yourself. If you toss two coins, what is the probability of getting 1 head and 1 tail?
Find the probability of rolling 3 on both of two number cubes.

Let’s say you want to toss two number cubes and find the possibility of getting a 3 on both of them. Each number cube has the numbers 1 through 6. The probability of rolling a 3 on one number cube is 16. What is the probability of rolling a 3 on both number cubes? If you roll a 1 on the first cube, you can roll any of the 6 numbers on the second roll. The same pattern continues if you roll a 2 on the first cube. You can make a table, like the image you see on the right, to show all of the possible outcomes. There are 36 possible outcomes. The outcome 3, 3 is only in the table once. So the probability of rolling two 3’s on the number cubes is 136. The probability of getting each event on its own is 16. If you multiply 16 × 16 you also get 136. For compound events like this, you can multiply the probabilities of the two events to find the probability of the compound event. Try this one yourself. What is the probability of tossing a 4 and then a 6 on a number cube?
Calculate the probability of picking a certain outfit.
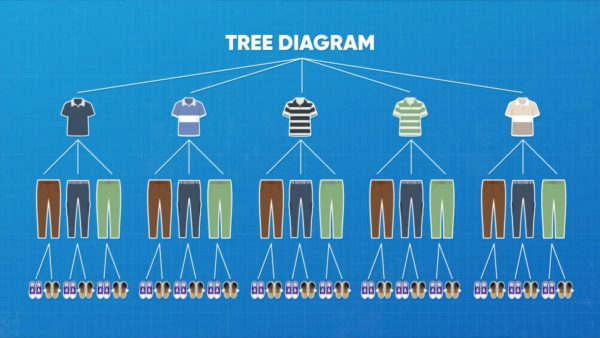
Let’s say you have 5 different shirts, 3 different pairs of pants, and 2 different pairs of shoes. You want to find the probability of picking the blue shirt, the blue pants, and the blue shoes if you choose at random. Make a tree diagram to show all of the possible outcomes. You start with a row that contains a list of the five possible shirts. Now you connect each different shirt with 3 different pants by drawing 3 branches from each shirt. And then you branch out again with 2 branches from each pants for the two different shoe possibilities. You can see from the tree diagram that there are 30 possible outcomes and only one of them is {blue shirt, blue pants, blue shoes}. So the probability of choosing the blue shirt, the blue pants, and the blue shoes is [ggfrac]1/30[/ggfrac]. You could also multiply [ggfrac]1/5[/ggfrac] × [ggfrac]1/3[/ggfrac] × [ggfrac]1/2[/ggfrac] to find the same probability of[ggfrac]1/30[/ggfrac]. Try this one yourself. Your friend has 3 shirts {blue, red, yellow}, 2 pairs of pants {brown, gray}, and 2 pairs of shoes {white, black}. What is the probability of randomly choosing an outfit and getting the red shirt, the gray pants, and the black shoes?
Calculate the probability of picking two dogs from a pet store.

Let’s say Amari and Emily are at a pet store and they each want to get a dog. The pet store has 4 dogs and 8 cats. Find the probability of both friends picking a dog if they choose a pet at random. These two events are not independent of each other. The probability of the second event is dependent on what happens in the first pick. In the first event, there are 12 total pets and 4 possible ways to get a dog. If Amari picks first, the probability that she picks a dog it 4 out of 12, or [ggfrac] 4/12[/ggfrac]For Emily, there are now 11 pets and 3 possible ways to pick a dog. The probability that Emily picks a dog is 3 out of 11, or [ggfrac] 3/11[/ggfrac]. You can multiply to find the probability of the friends picking two dogs. [ggfrac]4/12 [/ggfrac] × [ggfrac]3/11 [/ggfrac] = [ggfrac] 12/132[/ggfrac], or 0.9.9.9... You can state the probability as a percent and round it to the nearest tenth of a percent. The probability of Amari and Emily both getting dogs is 9.1%. Try this one yourself. In Amari and Emily’s situation, what is the probability of both friends getting cats instead of dogs?
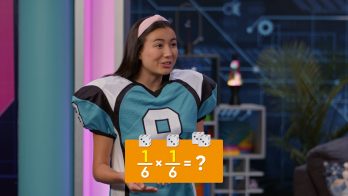
































































































































 Select a Google Form
Select a Google Form






 GENERATION GENIUS
GENERATION GENIUS




