Percents are special ratios where the whole is always 100. You use the % symbol to represent “percent.” 5 out of 100 or 5 : 100 is 5%.
To better understand percents…
LET’S BREAK IT DOWN!
Playing Basketball

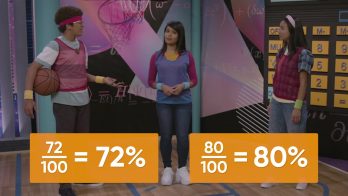
Amari and Emily are shooting hoops. Amari scored 72 out of 100 shots. Emily scored 80 out of 100 shots. How can you represent these as ratios and percents? A ratio is a relationship between two numbers. Ratios can be part-part or part-whole. Because we are looking at the number of scores (part) out of the number of shots (whole), we know that the ratio is part-whole. This is important because percents can only represent part-whole ratios. We can represent Amaris score as 72 :100 or [ggfrac]72/100[/ggfrac] or [ggfrac]72/100[/ggfrac] or 72%. We can also represent Amari's score as a decimal number where 1 is the whole, as 72 hundredths or 0.72. Try this yourself: What are all the ways you can represent Emily's score? What is her score as a percent and as a decimal?
Class Lunch
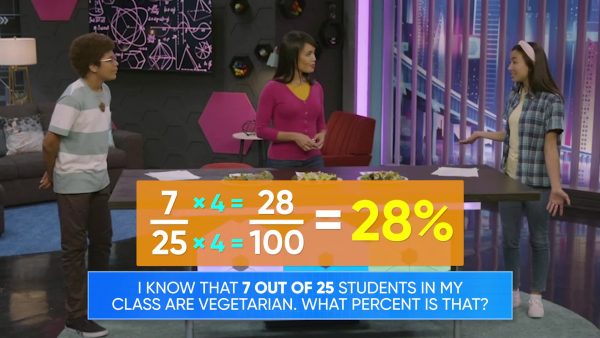
We are going on a class trip to the local science museum and need to plan for lunch. We surveyed the food preferences of the class, and 5 out of 20 students said they are vegetarian. We can represent this ratio as 5 :20 or [ggfrac]5/20[/ggfrac] or [ggfrac]5/20[/ggfrac]. But how do we represent this ratio as a percent? First we need to convert our ratio to an equivalent ratio out of 100. To make an equivalent ratio we multiply both parts of the ratio by the same number. We know that 20×5=100, so we need to multiply the numerator by 5 as well: 5×5=25. That means the equivalent ratio is 25:100 or [ggfrac]25/100[/ggfrac] or 25%. So 25% of the students in the class are vegetarians. Try this yourself: 7 out of 25 students in Emily's class are vegetarian. What percent of her class is vegetarian?
Calculating Homework

Emily has already read 80% of the books she needs for the year, and she has read 8 books. How many total books does she need to read this year? First, set up a ratio for this situation. Emily has read 8 out of an unknown total number of books, so we can write that as [ggfrac]number of books read /total number of books she needs to read[/ggfrac], or [ggfrac]8/n[/ggfrac]. We know that the number or books she has read is 80% of the total books, so we can set up an equation: [ggfrac]8/n[/ggfrac]=[ggfrac]80/100[/ggfrac]. We need to multiply the numerator and denominator of our ratio by the same number to keep the ratios equivalent. We know that 8×10=80, so n×10=100. That means n must equal 10. The total number of books Emily needs to read is 10. Try this yourself: Amari has read 90% of the books she needs for the year, and she has read 18 books so far. How many total books does she need to read this year?
Planting a Garden

We can also find the amount of a part for a given percent. We need to plant a garden with 20 plants in total, and 85% of the plants need to be fruit plants. We start by setting up an equation with the information we already know: [ggfrac] number of fruit plants/ total number of plants[/ggfrac]=[ggfrac]percent/100[/ggfrac]. Then we fill in the values we know, to get [ggfrac]n/20[/ggfrac]=[ggfrac]85/100[/ggfrac], where n represents the number of fruit plants. We can solve this problem by multiplying both the numerator and denominator by the same number. We can see that 20×5=100, so n×5=85. Now we need to find the value of n. We know that 17×5=85, so n must equal 17. We need to have 17 fruit plants in the garden. Try this yourself: If you are planting a garden with 25 plants, and 72% need to be vegetables, how many vegetable plants do you need?

























































































































 Select a Google Form
Select a Google Form






 GENERATION GENIUS
GENERATION GENIUS




