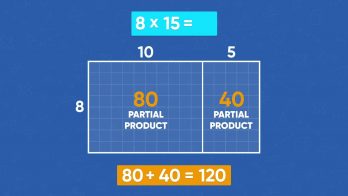
An area model shows multiplication by giving the factors as side lengths of a rectangle. The product is the area of the rectangle. An area model makes things simpler by allowing you to divide the rectangle into smaller rectangles whose area is easier to find.
To better understand multiplying up to 4 digits…
LET’S BREAK IT DOWN!
Camping

Multiplying a 1-digit number by a 2-digit number can help you find how many snacks you need for a camping trip. Let’s say you are going camping for 6 days and you need 28 snacks a day for the group. How many snacks do you need altogether? We can figure this out by thinking of 28 as 20 + 8. We can multiply 6 × 20 = 120 and 6 × 8 = 48. Then we can add the products: 120 + 48 = 168. You need 168 snacks. Try this one yourself: You and your friends are headed to a carnival. There are 7 of you. Each person needs 43 tickets to ride all the rides. How many tickets do you need in total so that everyone can ride all the rides?
Millipedes

Multiplying a 1-digit number by a 3-digit number can help you find how many total legs a group of millipedes has. Let’s say you see 3 millipedes and each millipede has 142 legs. How many legs do you see? We can figure this out by thinking of 142 as 100 + 40 + 2. We can multiply 3 × 100 = 300, 3 × 40 = 120, and 3 × 2 = 6. Then we can add the products. 300 + 120 + 6 = 426. There are 426 legs. Try this one yourself: You are on a hike and you see 7 millipedes. Each millipede has 142 legs. How many legs do you see in all?
Soccer Stadium

Multiplying a 1-digit number by a 4-digit number can help you find how many seats there are in a stadium. Let’s say the stadium has 4 sections. Each section has 2,316 seats. How many seats does the stadium have altogether? We can figure this out by thinking of 2,316 as 2000 + 300 + 10 + 6. We can multiply 4 × 2,000 = 8,000, 4 × 300 = 1,200, 4 × 10 = 40, and 4 × 6 = 24. Then we can add the products: 8,000 + 1,200 + 40 + 24 = 9,264. There are 9,264 seats. Try this one yourself: You need to decide if there are enough seats in the stadium for all fans to attend. There are 3 trains, and each train brings 3,104 people to the stadium. How many seats does the stadium need for all the people on the trains to attend? Does the stadium have enough seats?
Record Collection

Multiplying a 2-digit number by a 2-digit number can help you find how many records there are in a collection. Let’s say there are 14 boxes of records and each box contains 38 records. How many records are in the collection? We can figure this out by thinking of 14 as 10 + 4 and 38 as 30 + 8. We can multiply 10 × 30 = 300, 10 × 8 = 80, 4 × 30 = 120, and 4 × 8 = 32. Then we can add the products: 300 + 80 + 120 + 32 = 532. There are 532 records in the collection. Try this one yourself: You find 23 boxes of records in the garage. Each box contains 35 records. How many records do you have in all?
































































































































 Select a Google Form
Select a Google Form








