Intro to Quadrilaterals and their Attributes

Building a Community Center Let's say that the mayor of your town wants your help planning a community center. The mayor says that you can build a pool, a skate park, or a playground at the community center. The only rule is that whatever you build must be in the shape of a quadrilateral. A quadrilateral is a closed shape that has four straight sides. When you look at the drawing for the pool, you count eight sides. Is the pool a quadrilateral? No, it is not, because it does not have four sides. Next, you look at the drawing of the skate park and you see curvy sides. Is the skate park a quadrilateral? No, it is not because it does not have all straight sides. The playground is a closed shape with four straight sides, so it is a quadrilateral! The playground can go in the community center. It is important that when you group a shape into a category, the shape shares all of the attributes of the category. Try this one yourself: Will the mayor approve the community band's request to put a six-sided gazebo in the community center?

Framing Your Best Picture Let's say you have a bunch of oddly-shaped pictures that you would like to put into picture frames. You buy a package of frames that have all different shapes and every shape is a quadrilateral. The easiest way to frame your pictures is to match the attributes of the pictures to the attributes of the frames. The frame with four square corners is a rectangle. Your picture in the shape of a rectangle can go into this frame. Your picture that has four square corners and four equal sides is a square, and that picture can go in a square frame. The next picture you select looks like a square—because all of the sides are the same length—but it is tilted over. This picture is in the shape of a rhombus, a quadrilateral with four equal sides. You can put it in the rhombus-shaped frame. The next picture has opposite sides of equal length and these sides stay the same distance apart, which means they are parallel to each other. This picture is in the shape of a parallelogram, a shape with two sets of parallel sides. Try this one yourself: Why does a rectangle-shaped picture fit in a square frame?

Airplane Wings Now let's say you want to identify the name of the shape of an airplane wing. The wing's shape has four sides, so it is a quadrilateral. But, it is not a parallelogram since it has only one set of parallel sides. The airplane wing is in a shape called a trapezoid. Trapezoids are quadrilaterals that have exactly one pair of parallel sides. A trapezoid is different from a rectangle, square, rhombus, and parallelogram, because each of those shapes has two pairs of parallel sides. Did you know that the trapezoid shape of an airplane’s wing is super important because it helps the plane soar through the air? Desks are also often trapezoids because many desks have exactly one pair of parallel sides. Try this one yourself: What is another attribute that rhombuses and squares share, in addition to having two pairs of parallel sides?

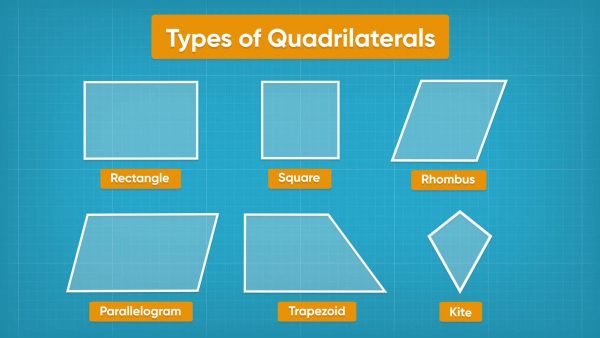
Putting Shapes into Categories Let's say we want to compare all the shapes we have learned about today. We would like to classify quadrilaterals according to which of the following attributes they share: one set of parallel sides, two sets of parallel sides, four right angles, all equal side lengths. Some quadrilaterals have just one set of parallel sides, and these are called trapezoids. Some quadrilaterals have two sets of parallel sides. These quadrilaterals are called parallelograms, and squares, rectangles, and rhombuses fit into this category. There is one other type of quadrilateral called a kite, which has no parallel sides and two pairs of sides next to each other with the same length. Kites go in a group all by themselves. Since all of these shapes we have looked at today are closed shapes with four straight sides, they are all quadrilaterals. Try this one yourself: What is the most specific category for a shape that has four right angles and two pairs of parallel sides?