We will learn how to partition a whole into halves, thirds, sixths, and eighths and how to represent those fractions as points on a number line.
To better understand fractions using the number line…
LET’S BREAK IT DOWN!
Making a Mural
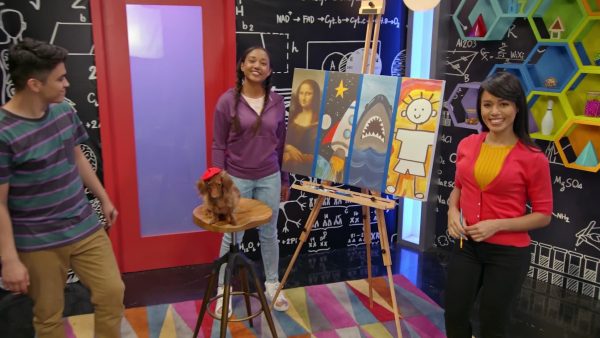
A mural is a painting often made by a group of people. Adesina, Marcos, April, and their puppy all want to work on a mural. There are four of them altogether. How can they split, or partition, the mural into four equal parts? Let’s think of the canvas as a number line with 0 on the left side and 1 on the right side. That way, the canvas is one whole. Next, let's partition the canvas into two equal pieces. The line in the middle represents [ggfrac]1/2[/ggfrac], where the top number (numerator) represents the number of parts to the left, and the bottom number (denominator) represents the total number of parts we partitioned the whole into. Next, let’s partition each part in half again. Now we have partitioned our whole canvas into four equal parts, so the denominator of our fraction will be four. As we count from the left to the right, we will collect parts in our fraction. The first mark is [ggfrac]1/4[/ggfrac] because we have one of the four equal parts on the left. The next mark is [ggfrac]2/4[/ggfrac] because we have two out of four equal parts on the left. Try this one yourself: What are the fractions for the third and fourth mark on our canvas number line?
Planning a Hike

Adesina, April, and Marcos are going on a hike. Looking at a map, they can see that the hike will be pretty intense. It is important that they take water breaks. Marcos suggests they take two water breaks, and April suggests they space them out evenly on the hike. Thinking of the hiking path as a number line, how can they space their two breaks evenly? They can partition their whole hike into three equal parts. Partitioning the route into three equal parts means the denominator of our fraction will be three. When they take their first water break, they will have completed one part of the hike, so the fraction is [ggfrac]1/3[/ggfrac]. Try this one yourself: What fraction of the hike will be complete when they take their second water break?
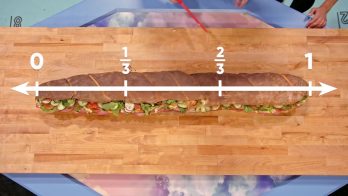
Eating a Giant Sandwich

Adesina, April, and Marcos are getting ready for lunch, but the sandwich they ordered is huge. It is six feet long. They all agree that a six-foot sub is too much for them to eat on their own and decide to partition it into three equal parts. To do this, they think of their sub as a number line, with 0 on the left and 1 on the right. This way, their whole sub is one whole on the number line. Marcos cuts the sub into three equal pieces. The first cut has one out of three pieces to the left, so that fraction is [ggfrac]1/3[/ggfrac]. The second cut has two out of the three pieces to the left, so that fraction is [ggfrac]2/3[/ggfrac]. The pieces are still too big, so Marcos cuts each third in half. Now the sub is cut in six equal parts, so the denominator of our fractions will be six. The first cut has one out of six pieces to the left, so that fraction is [ggfrac]1/6[/ggfrac]. The second cut has two out of six pieces to the left, so that fraction is [ggfrac]2/6[/ggfrac]. Try this one yourself: What fractions do the rest of the cuts represent on this sandwich number line?
Playing a Song with Fractions

Musicians need to know what notes to play and how long to play them. There are whole notes, half notes, and quarter notes. All notes are played for a fraction of the time a whole note is played. Let’s imagine the whole note is on a number line. Compared to the whole note, a half note is played for half the time the whole notes are played, so two half notes together last the same amount of time as a whole note. On a number line, the space between 0 and 1 is partitioned into two equal pieces. For quarter notes, you can play four notes in the same amount of time as the whole note. On a number line, the space between 0 and 1 would be partitioned into four equal pieces. Try this one yourself: How many eighth notes can you play in the time it takes to play one whole note? Draw and label the number line that represents eight notes.

























































































































 Select a Google Form
Select a Google Form






 GENERATION GENIUS
GENERATION GENIUS




