An algebraic expression is an expression that includes a variable. A variable is a letter that we use to represent an unknown value. For example, 3x + 2 is an algebraic expression because of the variable, x. You can use algebraic expressions to represent situations where there is some information that you do not know.
To better understand algebraic expressions…
LET’S BREAK IT DOWN!
An Algebraic Expression Contains an Unknown Amount

An algebraic expression can include numbers, operations, and variables. Let’s say a piggy bank has at least $4 in it, but there’s some unknown amount more than that in the bank. You can use the algebraic expression 4+x to represent the total amount of money in the piggy bank, where x represents the unknown amount. If the unknown amount turned out to be $6, then you could evaluate the expression 4+x by substituting 6 for x. The result is 4 + 6 = 10, so there is $10 in the piggy bank. Try this one yourself: Evaluate the algebraic expression x – 8 when x = 15.
There are Different Types of Expressions and Equations

A numerical expression does not contain variables. You can evaluate basic numerical expressions, such as 5 + 8 or 3 × 6, to a single number. This is called “simplifying.” An algebraic expression includes at least one unknown (variable). In earlier grades, you might have represented the unknown by an empty square, a fill-in-the-blank line, or a question mark. It’s common for the unknown to be represented with the variable x, but it could just as easily be some other letter, such as y or b. Expressions can contain different operations, such as x+4 for “four more than x,” 8-z for “z less than eight,” 2.5y for “two and one half times y,” and m3 for “m divided by three.” When two expressions have the same value, they can be set equal to each other. This creates an algebraic equation. For example, x+5=2x is an equation stating that the value of x+5 is the same as the value of 2x. Try this one yourself: Write an algebraic expression for “the sum of x and 10.”
Expressions Can Have Different Parts

Sometimes expressions contain more than one operation. Parts of an expression that are separated by addition or subtraction signs are called “terms.” The expression 3x+5 represents “three times x plus 5”. That is, 3 is multiplied by an unknown number and then five is added to the result. This expression has two terms: 3x and 5. Expressions can be longer and have more terms. The expression 8x+7-3x+8 has four terms: 8x, 7, 3x, and 8. Some of these terms contain the variable x, but others do not. When a term contains a variable, as in the terms 8x and 3x, the number multiplied by the variable is called the “coefficient”. When a term has no variable, as in the terms 7 and 8, the number is called a “constant”. The expression 2x+5 has two terms, 2x and 5. The first term has coefficient 2 and variable x. The second term has constant 5. Try this one yourself: Identify the terms, coefficients, and constants in the expression 4x+6y+9.
You Can Combine Like Terms

When an expression contains like terms, we can combine the terms to simplify the expression. When terms have no variables, this is obvious. The expression 9+5 has two constant terms, so simplifies to 14. A more complicated expression such as 8x+2x+4+9 has two x-terms and two constant terms. We can combine like terms with like. So, 8x + 2x = 10x, and 4 + 9 = 13. So 8x + 2x + 4 + 9 simplifies to 10x+13. When the expression includes subtraction, be careful to use the subtraction sign with the number immediately after it. The expression 5x-3+2x is the same as (5x + 2x) – 3 = 7x – 3. To simplify an expression that contains more than one variable, we still only combine terms with the same variable. For example, simplify 2x+5-x+y-2. Combine like terms: (2x – x) + y + (5 – 2) = x + y + 3. Try this one yourself: Simplify the expression: 3x+9-2+x+5y-6.
Algebraic Expressions Can Represent Buying Things

Let’s say you're ordering pizza. You order 2 pizzas for an unknown number of dollars each. You can represent this situation with the expression 2x, where x is the cost of each pizza. If you also buy a drink for $3, the total cost is 2x+3. If it turns out that each pizza costs $10, you can evaluate the expression for x=10. Calculate (2×10)+3 for a total of $23. Try this one yourself: Three packs of gum each started with the same number of pieces of gum, x, and you already chewed 5 pieces. Write an algebraic expression for the number of pieces of gum left in the packs. Then evaluate your expression, assuming there were 8 pieces of gum in each pack before you chewed any of it.
Careers That Use Algebraic Expressions

A seismologist studies earthquakes. Seismologists set up algebraic expressions to determine the amount of damage an earthquake could do to a city based on the earthquake’s size and distance from the city. Business owners who sell clothes set up algebraic expressions to find out how much money they will make based on the number of items they sell and the price of those items. Filmmakers who make movies use algebraic expressions to predict how many movie tickets they must sell to make a profit on their films.
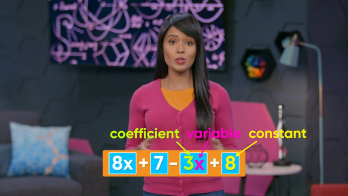
































































































































 Select a Google Form
Select a Google Form








