Identify Number Patterns (In Arithmetic and the Multiplication Table)

Odd and Even Socks Adesina, April, and Marcos are folding laundry. Each person has several socks, and they want to know how they can tell if it’s an even or odd number. If we can put all the socks into pairs, then there is an even number. April has 6 socks, and they can be put into 3 pairs, so 6 is even. Marcos has 8 socks, and they can all be paired up as well, so 8 is even. Combined, they have 14 pairs of socks, and 14 socks can all be paired up as well, so that number is even. They have just discovered a pattern: Even + even = even, since there are no left overs. Next, they fold socks that are a different color. This time, Marcos has 5 socks and April has 9 socks. 5 is an odd number because one of the socks is not paired. 9 is also an odd number because one of the socks is unpaired. But, if Marcos and Adesina put their socks together, now their unpaired socks make a pair together! Therefore, odd + odd = even. Next, they work on a new pile of socks. This time, Marcos has 6 socks and April has 5 socks. 6 is even, since Marcos' socks can all be paired. 5 is odd, since April has one sock left unpaired. If they combine their socks, one sock is still unpaired, and the answer is still odd. Therefore, odd + even = odd! Now you try: Without calculating, can you tell if 7 + 12 is odd or even?

Googly Eyes Adesina starts by putting 12 googly eyes into pairs. 12 can be put into 6 pairs, so 12 is even. If we subtract 4, which is an even number, then we have 8 googly eyes left, which is also even. Subtracting an even number from an even number doesn't leave any googly eyes unpaired. Even – even = even. If we try subtracting an odd number from an odd number, like 11 – 5 = 6, we end up with an even number! The unpaired googly eye in 11 is taken away by the unpaired eye in 5. Odd – odd = even. If we subtract an odd number from an even number, like 14 – 3 = 11, we get an odd number. Likewise, if we subtract an even number from an odd number, like 13 – 4 = 9, we also get an odd number. Then, even – odd = odd, and odd – even = odd. Now you try: Without calculating, can you tell if 21 – 9 is even or odd?

Multiplication Table Adesina, Marcos, and April are looking at a multiplication table. They notice some interesting number patterns: The row showing multiples of 2 contains all even numbers. All multiples of 2 are even! Looking at the row with multiples of 5, they notice that you add 5 each time you move along the row. All multiples of 5 end in 5 or 0. This is how you know you cannot divide 23 by 5: it doesn’t end in 5 or 0. Looking at the row with multiples of 10, we can see that all multiples of 10 end in 0. Discovering these patterns can help us check our work. Now you try: Is 73 divisible by 5? Is 90 divisible by 10? Is 43 divisible by 2?

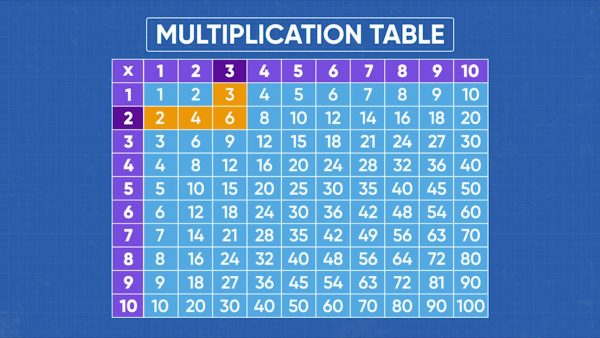
Multiplying Evens and Odds Let’s see what happens when we multiply using even and odd numbers. To find the product of two numbers, we can look up the two numbers on the multiplication table to see what they multiply to. 2 and 4 are even, and when we multiply them, we get 8, which is also an even number. Then, even × even = even. 1 and 3 are odd, and if we multiply them, we get 3, an odd number. Same with 5 × 7 = 35. Then, odd × odd = odd. 2 is even and 3 is odd, and if we multiply them, we get 6, an even number. Same with 6 × 9 = 54. Then, even × odd = even. Also, odd × even = even. Now you try: Without calculating, can you tell if 11 × 16 is odd or even?