How Many Triangles Can You Make? (Given Conditions)

When you are given three sides, they can form a maximum of one unique triangle. How many different triangles can you construct with sides lengths of 6, 8, and 10 inches? You can put the side lengths together in different orientations, but the triangle always has the same size and shape. All of the triangles you make are the same triangle. So if your three side lengths can form a triangle, they can only form exactly 1 unique triangle! Try this one yourself: How many unique triangles can you make with side lengths of 4, 6, and 8 inches?

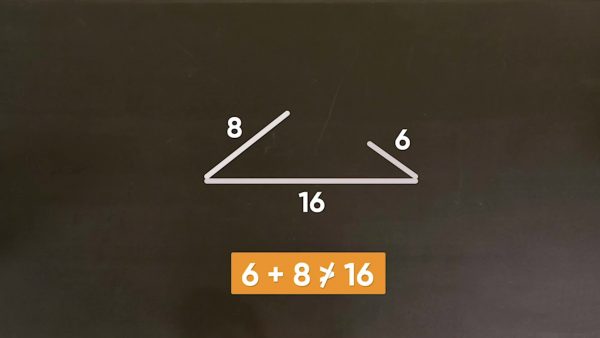
When you are given three side lengths, sometimes you cannot form any triangles at all. Next, let’s look at how many triangles you can form with side lengths of 6, 8, and 16 inches. If you put the longest side across the bottom, and the shortest side on the left, you can see that the other side is too short to connect the first two sides to form a triangle. That is because, in order to form a triangle, the two shorter sides together must be longer than the longest side. Mathematically speaking, the sum of the lengths of the two shorter sides of a triangle must be greater than the length of the longest side. Otherwise, they cannot form a triangle. Try this yourself: Given side lengths of 4, 8, and 12 meters, how many unique triangles can you make?

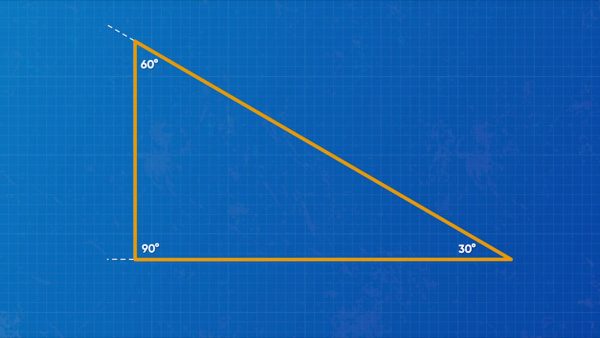
When you are given three angles, you can form either no triangles or infinitely many triangles. How many different triangles can you make with angle measures of 30 degrees, 60 degrees, and 90 degrees? To draw a triangle, use a protractor to make one of the angles. Make the side lengths as long or short as you want. At the end of one of the sides, make another angle, and join the sides together. You've made a triangle! Notice that you decided the side lengths. This means you could make a different decision. Because of this, you could make infinitely many different triangles with the same angles. Try this yourself: Given angle measures 100 degrees, 45 degrees, and 35 degrees, can you form one triangle, no triangles, or an infinite number of triangles?

When you are given three angles, you may not be able to form any triangles at all. Remember that the angles inside a triangle must add to 180°. 30° + 60° + 90° = 180°. What if you are given angles 45°, 20°, and 30°? 45° + 20° + 30° = 95°. These angles do not sum to 180°, so they cannot be used to form a triangle. Try this yourself: Given angle measures 60 degrees, 55 degrees, and 35 degrees, can you form one triangle, no triangles, or an infinite number of triangles?