The greatest common factor of two numbers is the greatest number that is a factor of both numbers. The least common multiple of two numbers is the least number that is a multiple of both numbers.
To better understand greatest common factor & least common multiple…
LET’S BREAK IT DOWN!
Use a number chart to find the LCM.
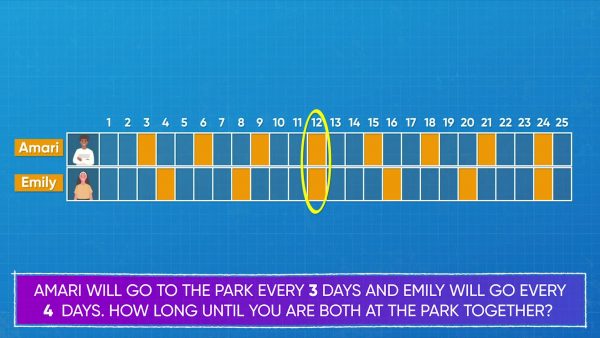
Amari goes to the park to practice basketball every 3 days. Emily goes every 4 days. After the first day, how long until they are both at the park together? Use can use a number chart to help. Color every 3: 3, 6, 9, 12, 15, 18, 21, 24. Then color every 4 days with a different color: 4, 8, 12, 16, 20, 24. On day 12 and day 24, both Amari and Emily are at the park. 12 and 24 are both common multiples of 3 and 4. 12 is the least of the common multiples, so it's called the least common multiple or LCM. Amari and Emily are at the park together after 12 days. Try this one yourself: Use a number chart or list to find the LCM of 5 and 4.
List multiples to find the LCM.

You can also list multiples of each number to find the LCM. Let's say you're watching a car race. Car A arrives at the pit stop every 15 minutes. Car B arrives at the same stop every 20 minutes. If both cars are at the stop now, how long until they are both at the stop again? Solve this problem by finding the least common multiple (LCM) of 15 and 20. First, find multiples of 15: 15 × 1 = 15, 15 × 2 = 30, 15 × 3 = 45, 15 × 4 = 60, etc. Find multiples of 20: 20 × 1 = 20, 20 × 2 = 40, 20 × 3 = 60, etc. You can see that 15 × 4 = 60 and 20 × 3 = 60. 60 is the first number to appear in both lists, so 60 is the least common multiple of 15 and 20. The cars arrive at the pit stop together after 60 minutes. Try this one yourself: List multiples to find the LCM of 4 and 10.
Use the greatest common factor to plan a BBQ.

Let's say you have 18 mini burgers and 24 mini hotdogs. You want to make plates for all of your friends that have the same amount of each food on each plate. You also want to make sure that there is no food leftover! What is the greatest number of plates you can make? You can use the greatest common factor (GCF) to solve this problem. First, list all of the factors of 18: 1, 2, 3, 6, 9, 18. Then, list all of the factors of 24: 1, 2, 3, 4, 6, 8, 12, 24. 6 is the greatest number that appears in both lists, so 6 is the greatest common factor. 6 × 3 = 18. 6 × 4 = 24. You can make 6 plates that each have 3 mini burgers and 4 mini hotdogs. Try this one yourself: Find the greatest common factor (GCF) of 12 and 20.
Use the GCF to plan sports teams.

A summer camp has 36 students and 20 counselors who want to play sports. They need to be sorted into teams so that there are the same number of students and the same number of counselors on each team. What is the greatest number of teams that you can make with no one left over? How many people are on each team? You can use the GCF to solve this problem. List the factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36. List the factors of 20: 1, 2, 4, 5, 10, 20. 4 is the greatest number in common between the two lists, so 4 is the greatest common factor (GCF). You can make 4 teams. 4 × 9 = 36, so there are 9 students on each team. 4 × 5 = 20, so there are 5 counselors on each team. Try this one yourself: Find the GCF of 14 and 21.
When do you use GCF and when do you use LCM?

Which process you need to follow depends on what the problem asks. There are clues to help you decide if GCF or LCM can help you solve the problem. If a problem talks about grouping items equally (with none leftover), you may need to use GCF to solve the problem. Another clue for GCF is keywords like 'greatest' and 'most.' If a problem talks about something that happens repeatedly or trying to figure out when something will happen at the same time, you may need to use LCM to solve the problem. Another clue for LCM is keywords like 'least' and 'minimum.' Try this one yourself: Sazi started a music machine that plays a drum sound every 2 beats and a horn sound every 3 beats. How many beats until the two sounds play at the same time? Did you need to use LCM or GCF to solve the problem?

































































































































 Select a Google Form
Select a Google Form






 GENERATION GENIUS
GENERATION GENIUS




