Solving algebraic inequalities is similar to solving algebraic equations. You apply inverse operations to isolate the variable on one side. However, there isn’t only one solution to an inequality, but a set of solutions.
To better understand algebraic inequalities…
LET’S BREAK IT DOWN!
There are 4 types of inequality symbols.

When talking about inequalities, there are 4 kinds of symbols: < 'less than', > 'greater than', 'less than or equal to', and 'greater than or equal to.' For example, x < 40 means that x can be any value that is less than 40, but it cannot be 40 itself. x 5 means that x can be 5 or any value greater than 5. Try this one yourself: b To enter an amusement park ride, you must be 85 cm or shorter. Represent that as an algebraic inequality, where x is the height of a person who wants to ride.
Solve an algebraic inequality to pack your suitcase.
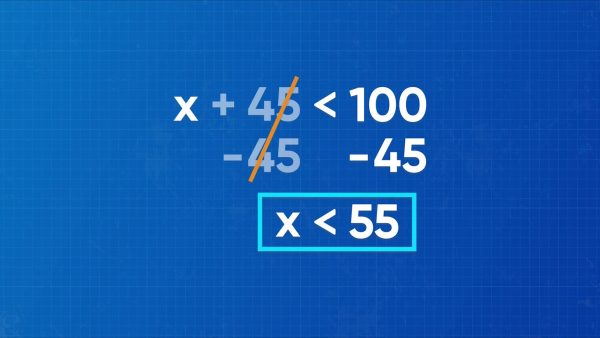
You are packing a suitcase for a trip. To go on the plane, your bag needs to weigh less than 100 lbs. You already put some things in your suitcase, and it now weighs 45 lbs. Set up an inequality to represent how much weight can be added. The unknown amount of pounds plus the 45 lbs. already packed must be less than 100 lbs: x+45<100. Solve the inequality using rules that are very similar to solving equations. Treat the less than sign as an equal sign. To isolate the x, subtract 45 from both sides to get x<55. Then the number of pounds you can add to the suitcase must be less than 55! 55 lb or more would be too much. Try this one yourself: Solve the inequality: x – 12 > 30.
Solve an algebraic inequality to have a successful bake sale.

You made cupcakes to sell at a school bake sale. You spent $48 on ingredients, and you charge $4 for each cupcake. How many cupcakes do you need to sell in order to make more money than you spent? To represent this as an equality, let the number of cupcakes sold be x. The amount of money that you get from customers is 4 times x, and it must be greater than $48 if you want to earn any profit: Solve 4x > 48. Divide both sides by 4 to isolate x: x> 12. Therefore, you need to sell more than 12 cupcakes to make more than you spent. Try this one yourself: Solve the inequality: 3x<42.
Solve algebraic inequalities that are inclusive.

You earn $8 per hour babysitting, plus you already have $12 saved up. How many hours do you need to work to have at least $100 saved up? Represent the amount of money you have with the inequality 8x+12≥100. The words "at least" say that 100 is included. Solve for x using inverse operations. First, subtract 12 from both sides to get 8x≥88. Next, divide both sides by 8 to get x≥11. That means that you need to work 11 hours or more to have at least $100. 11 is included in the answer, since working 11 hours means you have saved $100. Try this one yourself: Solve the inequality: 3x+9≥63.
Solve algebraic inequalities with fractions.
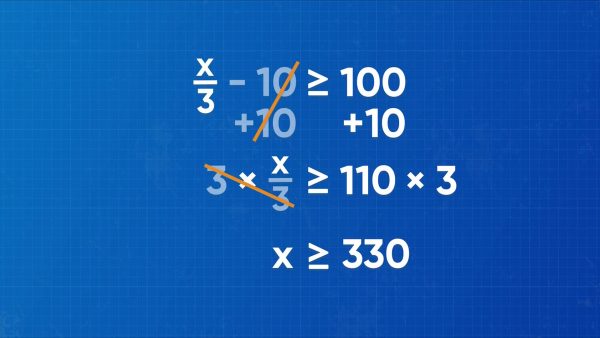
Your band is playing a concert, and you get to keep [ggfrac]1/3[/ggfrac] of the money made from ticket sales. You promised a friend $10 for helping move your gear. How much money needs to be made from ticket sales for you to have $100 at the end of the night? Let x represent the total earned from ticket sales. Then we can represent your earnings by the inequality [ggfrac]x/3[/ggfrac]-10≥100. To solve, add 10 to both sides then multiply both sides by 3. [ggfrac]x/3[/ggfrac]≥110. x=330. This means that you need to sell at least $330 worth of tickets to make at least $100. Try this one yourself: Solve the inequality x2+13≥27.


























































































































 Select a Google Form
Select a Google Form








