Find Factor Pairs within 100

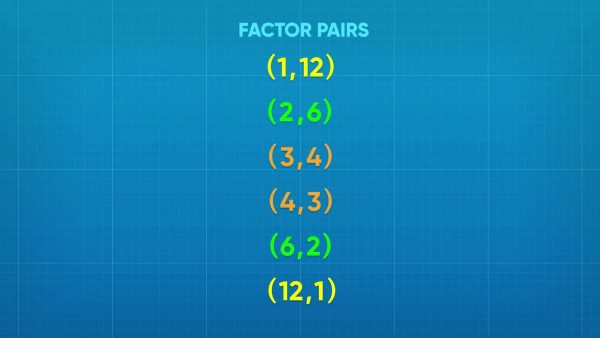
Relay Teams Let's say that you have twelve people and you would like to make teams to compete in a relay race. What are all the different ways you can put twelve people into equal-sized groups? One way to solve this problem is to think of all the different factors of 12. Starting with 1, since 1 × 12 = 12, we know that we can make one team with twelve players. We next consider 2, and since 2 × 6 = 12, we can have two teams of 6. Since 3 × 4 = 12, we can make 3 teams with 4 people in each, and 4 teams with 3 players each, since 4 × 3 = 12. Five does not divide evenly into 12, but 6 × 2 = 12, so we can make 6 teams with 2 players each. We continue testing the next whole numbers, and find that 7, 8, 9, 10, and 11 don't divide evenly into 12. Finally, we can have 12 teams each with 1 player, since 12 × 1 = 12. These are all of the different ways to make teams from 12 people, and also all of the factor pairs of 12. Try this one yourself: How many different ways can you put 16 books into piles, where each pile has the same number of books.

Karate Mats Let's say that you have 30 karate mats that need to be arranged into a rectangle. These rectangles can help us to find the factor pairs for the number 30. We need to find all the ways to make rectangles with the mats with the same number of mats in each row. Starting with 1, we know that we can make 1 row with 30 mats, since 1 × 30 = 30. This means that 1 and 30 are a factor pair of 30. If we make 2 rows, each row will have 15 mats, since 2 × 15 = 30. 2 and 15 are another factor pair. We can have 3 rows of 10 mats since 3 × 10 = 30, making 3 and 10 a factor pair. Four does not divide evenly into 30, but we can have 5 rows of 6 mats, since 5 × 6 = 30. We can also have a rectangle with 6 rows and 5 mats in each row, since 6 × 5 = 30. We notice that the 6 × 5 rectangle looks closest to a square, and closest to the 5 × 6 rectangle. This is when we know that we have found all the factor pairs, since the rectangle dimensions are reversing. Repeat the pattern to find the rest of the factor pairs. Try this one yourself: How many different large rectangles can be made from 12 smaller rectangles?

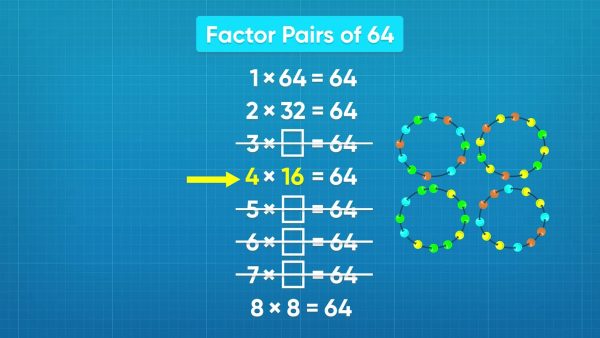
Beaded Bracelets Let's say you have 64 beads and you would like to split them up into equal groups to make bracelets. Finding the factor pairs for the number 64 will help us solve this problem. Starting with 1, we can make 1 bracelet with 64 beads (1 × 64 = 64), 2 bracelets with 32 beads each (2 × 32 = 64), 4 bracelets with 16 beads (4 × 16 = 64), and 8 bracelets with 8 beads (8 × 8 = 64). The other numbers between 1 and 8 do not divide evenly into 64. Once we see the same factor repeating in a factor pair—like we did with 8 × 8—we know that we have found all of the factor pairs. The factors begin to repeat after that, so we can stop. The factor pairs of 64 are 1 and 64, 2 and 32, 4 and 16, and 8 and 8. Try this one yourself: How many different ways can you divide 36 coins into bags with the same number of coins in each bag?

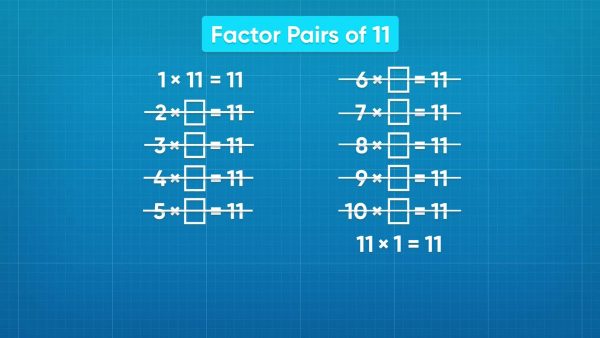
Prime Cupcakes Let's say that you want to use factor pairs to see how you can split 11 cupcakes into packs of the same number of cupcakes. We can use factor pairs to find out the different ways 11 can be divided into equal groups. Start at 1. We can have 1 pack of 11 cupcakes because 1 × 11 = 11. Try the other numbers: 2, 3, 4, 5, 6, 7, 8, 9, and 10. None of these number are factors of 11. None of them divide evenly into 11. We could have 11 packs with 1 cupcake each, since 11 × 1 = 11. That means 1 and 11 are the only factor pairs of 11. 11 is a prime number. A prime number is defined as a number whose only factors are 1 and itself. Try this one yourself: How many different teams, each with the same number of players, can you make from a class of 19 students?