A quotient is the result of division. Partial quotients are a method to solve larger division problems by breaking the process into multiple smaller division problems.
To better understand division using partial quotients…
LET’S BREAK IT DOWN!
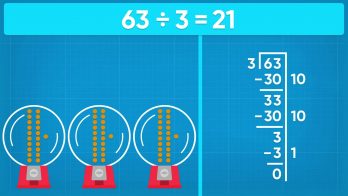
Gumball Machine

Let's say you have a gumball machine with 63 gumballs. You want to share these gumballs equally among 3 people. How many gumballs does each person get? You can solve this problem by giving each person one gumball at a time until they are all divided, but this would take a long time! Instead, you could give each person 2, 5, or even 10 gumballs at a time. If you give each person 10 gumballs, then you have shared 30 gumballs. There are 63 – 30 = 33 gumballs left to share. You could then share 10 more gumballs with each person, sharing another 30 gumballs. There are 33 – 30 = 3 gumballs left to share. If you give each person 1 more gumball then all the gumballs have been shared. Each person received 10 + 10 + 1 = 21 gumballs. We call 10, 10, and 1 "partial quotients." They are each a part of the final quotient. You can use the Big 7 method to record your work. You can make a big 7 and write the dividend and divisor at the top. On the outside of the 7, you record your partial quotients (10, 10, 1). On the inside of the 7, you record your subtractions. You can find different partial quotients for the same division problem. You could give each person 20 gumballs to start. There are 63 – 60 = 3 gumballs left. Then you could give each person 1 more gumball. They would each have 20 + 1 = 21 gumballs. Now you try: Use the Big 7 method to show how to share 63 gumballs between 2 people.
Hats for a School Party

Let's say you need 435 hats and want to order equal amounts of 6 different hat types. How many of each hat should you order? You can find the answer by finding 435 ÷ 6 =? Solve with partial quotients by making the big 7 and writing the 435 and 6 at the top. Think about different products you can make with 6 and another number. 6 × 50 = 300 is a number close to 435. Write 50 as a partial quotient and record 435 – 300 = 135 inside the 7. There is 135 left to divide. 6 × 20 = 120, so write 20 as a partial quotient and record 135 – 120 = 15 inside the 7. There is 15 left to divide. 6 × 2 = 12, so write 2 as a partial quotient and write 15 – 12 = 3 inside the 7. 3 is less than 6 so the 3 cannot be equally divided. The quotient is 50 + 20 + 2 = 72. 435 ÷ 6 = 72 with 3 remaining. If you want to order equal amounts of each type of hat and have at least 435 hats, you will need to order 73 hats of each type. Now you try: Use the Big 7 method to show how to order 385 hats of 2 different hat types.
Cake Pops

Let's say you've made 387 cake pops and you need to divide them equally onto 12 trays to serve at a party. How many cake pops should you put on each tray? You can find the answer by finding 387 ÷ 12 = ? Solve with partial quotients by making the big 7 and writing the 387 and 12 at the top. Think about different products you can make with 12 and another number. 12 × 20 = 240 is a number close to 387. Write 20 as a partial quotient and record 387 – 240 = 147 inside the 7. 12 × 10 = 120. Write 10 as a partial quotient and record 147 – 120 = 27 inside the 7. 12 × 2 = 24. Write 2 as a partial quotient and record 27 – 24 = 3 inside the 7. The quotient is 20 + 10 + 2 = 32 with 3 remaining. You could put 32 cake pops on each tray and then eat the 3 left over! Now you try: Use the Big 7 method to show how you can place 449 cake pops on 14 trays.
Money

Let's say you raised $5,325 for local charities. Way to go! You want to divide it equally among 25 different local charities. How much does each charity receive? You can find the answer by finding 5,325 ÷ 25 =? Solve with partial quotients by making the big 7 and writing the 5,325 and 25 at the top. Think about different products you can make with 25 and another number. 25 × 100 = 2,500, so write 100 as a partial quotient and record 5,325 – 2,500 = 2,825 inside the 7. Since 2,825 > 2,500, you can use 100 as a partial quotient again. Write 100 outside the 7 and record 2,825 – 2,500 = 325 inside the 7. 25 × 8 = 200, so write 8 as a partial quotient and record 325 – 200 = 125 inside the 7. 25 × 5 = 125, so write 5 as a partial quotient and record 125 – 125 = 0 inside the 7. The quotient is 100 + 100 + 8 + 5 = 213. There is no remainder, so each charity receives exactly $213. Now you try: Use the Big 7 method to show how you could share $2,016 equally among 18 charities.
































































































































 Select a Google Form
Select a Google Form








