You can use an area model to solve division problems by representing the number being divided as the area of a rectangle and the known factor as one of the side lengths. The quotient is the length of the other side.
To better understand division using an area model…
LET’S BREAK IT DOWN!
Counting Fossils

There are 78 fossils in April's fossil kit. In the kit, there are equal amounts of 6 different kinds of fossils. Solve 78 ÷ 6 to find out how many of each kind there are. You can use an area model to solve division problems. First, let's think back to how to solve a multiplication problem with an area model. For example, to find 6 ✕ 24, imagine a rectangle with a length of 24 units and a width of 6 units. The area inside the rectangle represents the answer to the multiplication problem. The length, 24, can be split up into its tens (20) and its ones (4). Since 6 ✕ 20 = 120, and 6 ✕ 4 = 24, the total area inside the box is 120 + 24, or 144 square units. That means 6 ✕ 24 = 144. Now let's get back to our division problem. Turn the division problem into a multiplication problem by asking 6 times what number is 78. Now show the problem with an area model. Imagine a rectangle. The length of one side of the rectangle is 6. The length of the other side is unknown. The area is 78. Split the area into two sections by splitting 78 into two sections using place value. One section has an area of 70 and the other section has an area of 8. Then, think about what number you can multiply by 6 to get close to 70. Multiplying 6 by 11 results in 66. Write 11 above the first section. Then subtract 70 – 66 = 4 to find the leftover area. Move the leftover area to the next section and combine it with the 8 in that section for a total of 12. What number can you multiply by 6 to get 12? That's exactly 2. Write 2 above the second section. Since 11 + 2 = 13, that means 78 ÷ 6 = 13. There are 13 of each type of fossil. Try this one yourself: Use an area model to divide 95 by 4. Compare your strategy and your answer with another student.
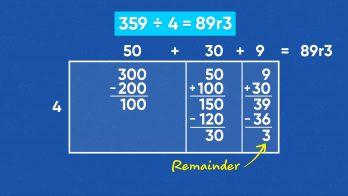
Planning a Pizza Party

Marcos and April are helping to organize a graduation party for their school. Based on a survey of all the kids and their guests, they need to order 359 pizzas. They need to order an equal amount of 4 different types. April divides 359 ÷ 4 to find how many of each type to order. She draws a rectangle with a width of 4. The length of the other side is unknown. She splits the rectangle into three sections: 300, 50, and 9. April knows that 4 ✕ 50 = 200, so she writes 50 above the first section of the rectangle. That leaves 300 - 200 = 100, so she adds 100 to the next section along with the 50 to get 150. April knows she can get close to 150. Since 4 ✕ 30 = 120, she writes 30 above the second section of the rectangle. That leaves 150 - 120 = 30, which she adds to the 9 in the last section to get 39. April can get pretty close to 39 because 4 ✕ 9 = 36. She writes 9 above the third section of the rectangle. Then she subtracts 39 – 36 = 3. She can’t split 3 into 4 equal groups, so 3 is the remainder. To find the answer, add up the lengths of all 3 sections: 50 + 30 + 9 = 89 with a remainder of 3. Since they need a little more than 89 of each type of pizza, they should round up and order 90 of each type of pizza. Try this one yourself: Use an area model to divide 267 by 7. Compare your strategy and your answer with another student.
Filling Egg Cartons

Some chickens laid 372 eggs. Adesina is putting the eggs into cartons. Each carton holds 12 eggs. How many cartons will there be? To find the number of cartons needed, divide 372 ÷ 12. Set up an area model. The area model is a rectangle. One side has a length of 12 and the other side is unknown. The model has 3 sections broken up by place value: 300, 70, and 2. For the first section, 12 ✕ 20 = 240. Write 20 above this section. That leaves 300 - 240 = 60 left over. Add 60 to the 70 already in the second section, for a total of 130. You can get close to 130, because 12 ✕ 10 = 120. Write 10 above this section. That leaves 130 - 120 = 10 left over. Add the leftover area, 10, to the 2 already in the third section to get an area of 12. 12 ✕ 1 = 12, so write 1 above this section. Since 12 – 12 = 0, there is no remainder. Add up the length to find the answer: 20 + 10 + 1 = 31. There will be 31 full cartons of eggs. Try this one yourself: Use an area model to divide 378 by 14. Compare your strategy and your answer with another student.
Ribbons

Adesina wants to make ribbon pins for school spirit week. She buys a spool of ribbon that is 5,629 centimeters long. Each pin needs 25 centimeters of ribbon. How many pins can she make? To find the number of pins she can make, find 5,629 ÷ 25. Set up a rectangle with four sections. The width of the rectangle is 25. Label each section with: 5,000, 600, 20, and 9. Since 200 ✕ 25 = 5,000, write 200 above the first section. For the second section, multiply 20 ✕ 25 to get 500. Write 20 above the second section. Then combine the leftover area, 600 - 500 = 100, with the 20 in the third section. Then figure out how many times 25 goes into 120. Since 4 ✕ 25 = 100, write 4 above the third section. The leftover area is 120 – 100 = 20. Combine the leftover 20 with the 9 in the fourth section. Since 25 goes into 29 once, write a 1 above the fourth section. Subtract 29 – 25 = 4. Since you can’t divide 4 into 25 evenly, there is a remainder of 4. So, the total number of ribbon pins that can be made is 200 + 20 + 4 + 1 = 225. Adesina just won't use the last 4 centimeters of ribbon. Try this one yourself: Use an area model to divide 3,368 by 15. Compare your strategy and your answer with another student.
































































































































 Select a Google Form
Select a Google Form








