What are the properties of shapes? 2D shapes are flat and can hold area. When all the sides are straight, the shape is a polygon. These shapes have properties like side lengths and angles.
To better understand classifying shapes in a hierarchy (quadrilaterals & triangles)…
LET’S BREAK IT DOWN!
Triangle Party

We are having a Triangle Party! We have many familiar objects, all with three straight sides. One is a chip with all equal length sides. Another is a sail for our model sailboat. It has three different side lengths and one 90° angle. We know that triangles can have acute angles, meaning angles smaller than 90°, obtuse angles that are bigger than 90°, or right angles that are equal to 90°. When the sides of a triangle are all the same length, it is equilateral. If only two are the same length, it is isosceles, and if all the lengths are different, it’s scalene. What kind of triangles are our objects? The chip is an equilateral triangle because of its three equal sides. The sail is a right scalene triangle because all the lengths are different, and it has a 90° angle. Try this yourself: What kind of triangle is a coat hanger if it has two equal-length sides and one angle larger than 90°?
Hanging Pictures
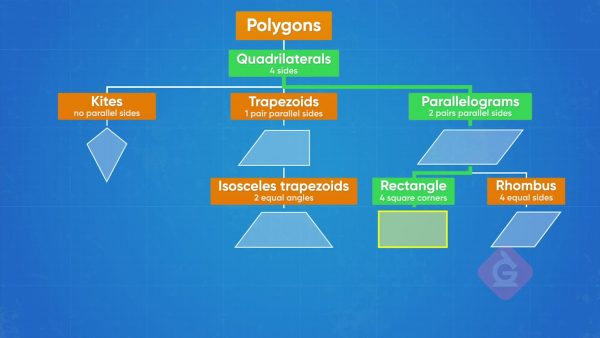
We are in art class and need to hang pictures in their matching frames with the same shape. All the frames are sorted into their most specific category of 2D shape, but we still need to sort the pictures. All the frames have four straight sides, so we know they are all quadrilaterals. Some frames have one set of parallel sides; these are trapezoids. Others have two sets of parallel sides; these are parallelograms. Some of the parallelograms have right angles, which means they are rectangles. Your friend points to a pile of frames that are parallelograms that have four equal sides but no right angles. Those are rhombi, or a rhombus if we only have one. The last pile is even more specific, with 4 right angles and 4 equal sides. Those are squares! Your first picture has four straight sides, two pairs of parallel sides with different lengths. That means the most specific category we can choose is a parallelogram. That is where we will find the matching frame! Try this yourself: There is a picture with four equal sides and no right angles. What is the most specific category of shape for the picture?
Packing for Summer Camp

Suppose you are packing for summer camp and decide to sort your belongings by shape. You have a book, a clothes hanger, and a kite. Looking at the shapes, you notice they all have straight edges, so you put them all in the polygon pile. The hanger has three sides, so you know it is a triangle. The book and kite both have four sides, so they are quadrilaterals. The book has all right angles, so it is also a rectangle. But what shape is the kite? It has straight sides, so it is a polygon. The kite has four sides, so it is also a quadrilateral. Even more specifically, it has two pairs of adjacent sides that are equal in length, which makes it a kite! Try this yourself: What are all the categories that a shape with four equal-length sides, no right angles, and no parallel sides could belong to?
Using a Hierarchy
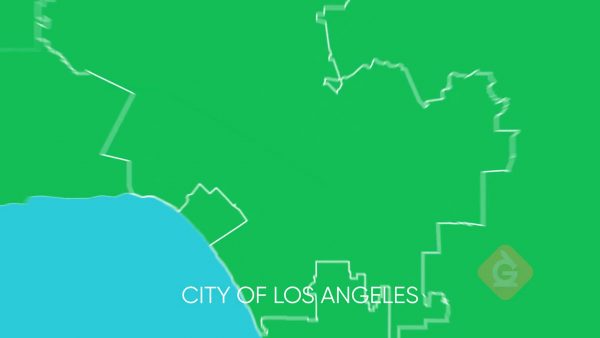
Sasha and Derek are trying to explain their location to a friend. Sasha says they are in Los Angeles, but Derek says they are in California. How do we know who is right? They both are! We can understand this using a hierarchy. At the highest level, they are in California. More specifically, they are in the city of Los Angeles. Even more specifically, they are in Hollywood! So, knowing that someone is in Hollywood, we also know that they are in Los Angeles and California because those are the levels above Hollywood in our location hierarchy. Try this yourself: Think about your school. What is its location hierarchy?
































































































































 Select a Google Form
Select a Google Form








