Area & Circumference of Circles

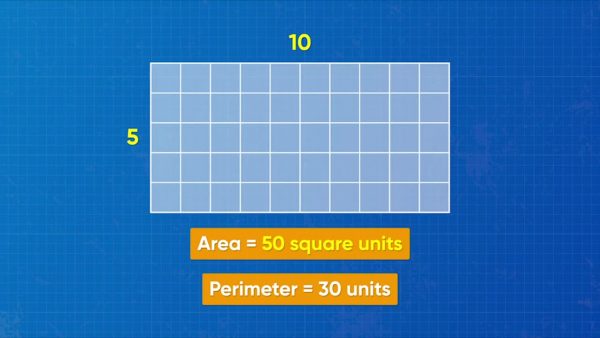
Review Perimeter and Area Perimeter is the distance around a shape. For example, a rectangle that is 5 units long and 10 units wide has a perimeter of 30 units. Area is the amount of space inside a 2D shape. Area is measured in square units. To find the area of the rectangle, multiply the length by the width. 5 units × 10 units = 50 square units. Try this one yourself: A rectangle has length 4 units and width 8 units. What is its perimeter? What is its area?

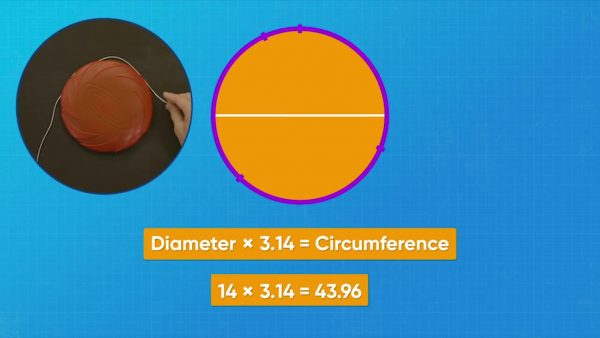
Circumference of a Frisbee In ultimate frisbee, the frisbee has to have a circumference of 66 centimeters. How can you find the circumference of a frisbee? Circumference is the distance around a circle. One way to find the circumference is to use a string. Measure around the frisbee with the string, and then measure the string with a meter stick. It is about 44 cm. What if you don’t have a string? You can calculate the circumference from the diameter. The diameter is the distance straight across a circle. The diameter always passes through the center point of the circle. The frisbee has a diameter of 14 cm. The circumference of a circle is always about 3.14 times the diameter. So the circumference of the frisbee is approximately 14 × 3.14 = 43.96 cm. The number 3.14 is an approximation. The actual number has a decimal that never ends. It is 3.141592653589793238.... This number is called pi. You can approximate pi as 3.14. You can always find the circumference of a circle by multiplying the diameter by pi. Try a small frisbee: the diameter is 7 cm, so the circumference is about 7 × 3.14 = 21.98 cm. Try a big frisbee: the diameter is 21 cm, so the circumference is about 21 × 3.14 = 65.94 cm. Pi is a ratio of the circumference of a circle to its diameter. If the diameter is 1 cm, then the circumference is about 3.14 cm. If the diameter is 2 cm, then the circumference is about 6.28 cm, and so on. Circumference divided by diameter equals pi. You can use letters instead of names: d for diameter and C for circumference. Try this one yourself: A circle has diameter 10 units. What is its circumference? Use 3.14 for pi.

Circumference of a Table A table border wraps around a circular table for decoration. The border is 15.7 feet long. How big is the diameter of the table if the border wraps around it perfectly? You know the circumference and now you need to find the diameter. Rearrange the equation C = πd. Divide both sides by π. On the right side, the pi symbols cancel out, since pi divided by pi equals 1. So, C ÷ π = d. Substitute 15.7 feet into the equation for C. Then evaluate: 15.7 ÷ 3.14 = 5. So, the table border fits around a table with diameter 5 feet. Try this one yourself: A circle has circumference 25.12 meters. What is the diameter of the circle? Use 3.14 for pi.

Area of a Circular Pen A tortoise lives in a circular pen. What is the area of the pen? Remember, area is the space inside a 2D shape. The area of a circle can be calculated with the formula A = π x r2, where r stands for radius. The radius is the measurement from the center of the circle to its edge. The radius is half of the diameter. So, to find the area of the pen, multiply pi times the radius squared. When you square a number, you multiply it by itself. The radius of the pen is 2 meters. In the formula, substitute in 2 for r. 22 = 2 × 2 = 4. Then, 3.14 × 4 = 12.56. So, the area of the pen is about 12.6 square meters. Where did the area formula come from? You can cut a circle into slices, like a pizza. Then, rearrange the pieces into a shape like a parallelogram. The area of a parallelogram is its base times its height. In this parallelogram-like shape, the height is the radius of the circle, or r. The base is half the circle’s circumference. The circumference is pi times the diameter, so half the circumference is pi times the radius, or π x r. So, the area of the shape is π x r x r, or π x r2. Try this one yourself: A circle has radius 3 meters. What is the area of the circle? Use 3.14 for pi.

Area of a Pool A circular pool has diameter 6 meters. What is its area? The formula for area is A = π x r2. Find the radius by dividing the diameter in half: 6 meters divided by 2 is 3 meters. So, the radius is 3 meters. Then, square the radius: 3 × 3 = 9. Then, multiply 9 × 3.14 = 28.26. The area of the pool is about 28 square meters. Try this one yourself: A circular pool has diameter 7 meters. What is its area? Use 3.14 for pi.