The angles in a triangle have a special relationship. This means that if you know the measures of two of the angles, you can predict the measure of the third. There are also special relationships between the angles made when a line intersects a pair of parallel lines.
To better understand angle relationships…
LET’S BREAK IT DOWN!
Review angle terminology.
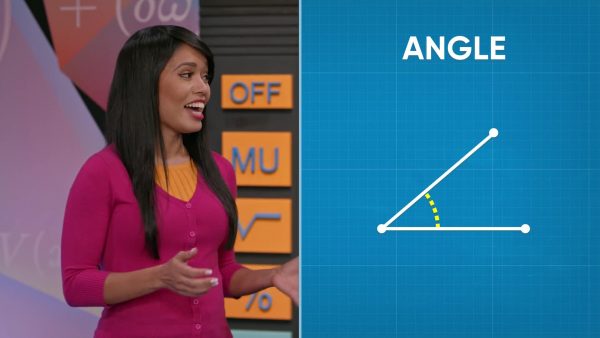
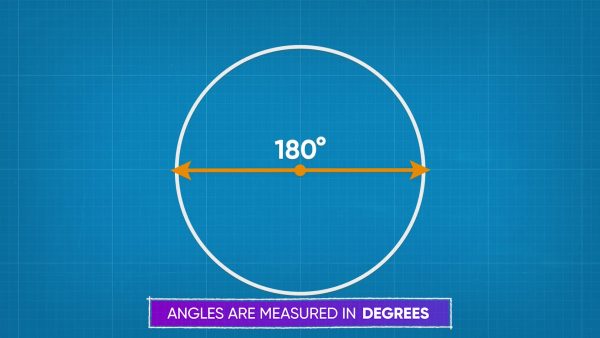
An angle measures the space between two rays, lines, or line segments. Angles are measured in degrees. A full circle measures 360°, a half circle 180°, and a quarter circle 90°. Try this one yourself: What is the measure of the angle of [ggfrac]3/4[/ggfrac] of a circle?
The sum of angles that form a line is 180°.
Take a straight line and intersect that line with another line. This makes two angles. Imagine that one of those angles measures 90°. What is the measure of the other angle? You know that both angles must add to 180°, since a straight line shows a 180° angle. So the other angle measures 180 – 90 = 90°. What if the first angle measures 60°? Then the other angle measures 180 – 60 = 120°. Two angles that add to 180° are called supplementary angles. Try this one yourself: One angle measures 75°. What is the measure of the second angle that forms a line with the first angle?
The sum of the angles in a triangle is 180°
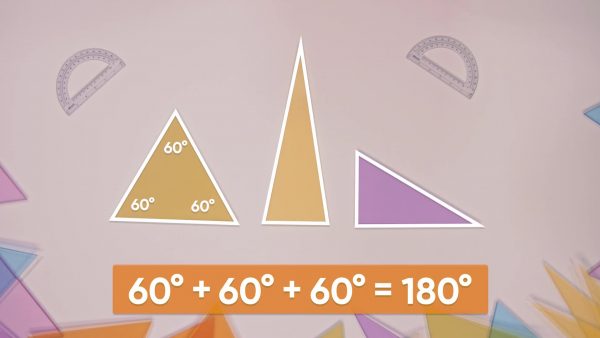
Imagine you have 3 copies of the same triangle. The angles are labeled A, B, and C. Rotate the triangles to put one of each copy of each angle together. It forms a straight line! Is the sum of the measures of the angles in a triangle 180°? To test this, Emily and Amari measure the angles in a set of three triangles. Triangle 1 has angles that measure 60°, 60°, and 60°. That is 180° in all. Triangle 2 has angles that measure 80°, 80°, and 20°. That is 180° in all. Triangle 3 has angles that measure 80°, 30°, and 60°. That's 180° as well! The measures of the 3 angles of a triangle always add up to 180°. That means, if you know two angles, you can find the measure of the third. A triangle has angles that measure 40° and 60°. What is the measure of the third angle? 180 – 40 – 60 = 80°. The last angle measures 80°. Try this one yourself: A triangle has angles that measure 70° and 45°. What is the measure of the third angle?
Vertical angles are always equal.
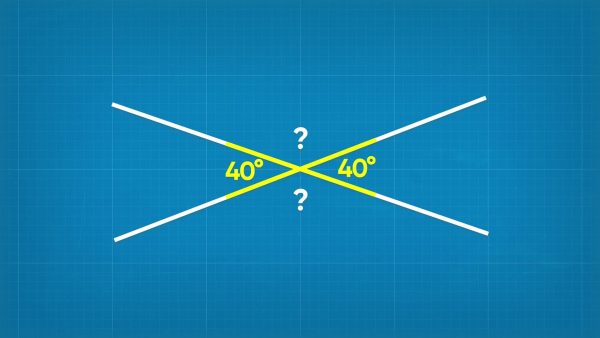
Imagine that you've drawn two lines that intersect. The measure of the angles that are opposite each other are always equal. These angles are called vertical angles. So, if you know one angle, you automatically know the other. If two lines cross, forming one angle that is 40°, the angle opposite that angle is also 40°.
A transversal is a line that crosses two parallel lines.
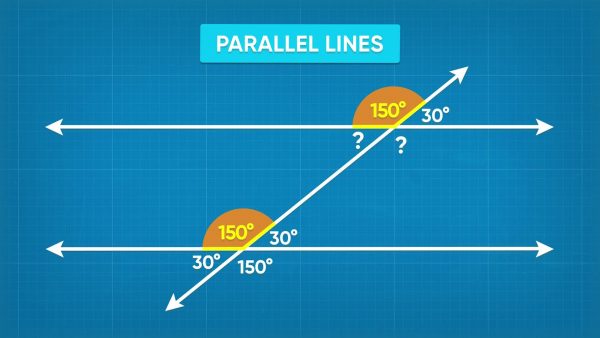
When a transversal crosses two parallel lines, the angles formed have special relationships. First, let's talk about some vocabulary. Angles that are in the same position on both intersections are called corresponding angles. Corresponding angles are always equal. Angles that are both on the inside of the parallel lines are called interior angles. Interior angles add to 180°. Angles that are both on the outside of the parallel lines are called exterior angles. Exterior angles add to 180°. Angles that are across from each other on different lines are called alternate angles. Alternate interior angles are always equal. Alternate exterior angles are also always equal! Using all of the relationships you've seen so far, knowing just one angle can help you find every angle formed by the intersecting lines. Try this one yourself: The measure of an angle formed by a transversal is 120°. What is the measure of the corresponding angle on the other line? What is the measure of the alternate exterior angle to the 120° angle?
































































































































 Select a Google Form
Select a Google Form






 GENERATION GENIUS
GENERATION GENIUS




