Add & Subtract Fractions (Like Denominators)

Review Before we begin adding and subtracting fractions, we need to review some key concepts we learned already: A fraction is a number that represents part of a whole. The number below the line is called the denominator and it tells us how many equal parts the whole is split into. The number above the line is called the numerator and it tells us how many parts we have. Now you try: If [ggfrac]4/6[/ggfrac] represents how many slices of a pie we have left, what do 4 and 6 represent?

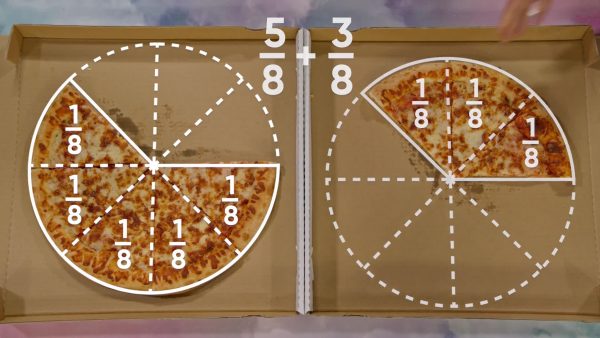
Pizza Marcos and April each have a pizza with 8 equal slices, and they ate part of their pizzas. Marcos has 5 slices left and April has 3 slices left. How can we represent leftover pizza as fractions? 5 out of 8 slices can be represented as [ggfrac]5/8[/ggfrac], and 3 out of 8 slices can be represented as [ggfrac]3/8[/ggfrac]. If we put both April and Marcos’ slices into an empty pizza box, they make one whole pizza together. This means that [ggfrac]5/8[/ggfrac] + [ggfrac]3/8[/ggfrac] = [ggfrac]8/8[/ggfrac], and [ggfrac]8/8[/ggfrac] is the same as 1 whole. We add the numerators, but we keep the denominator the same. The denominator only tells us how many slices the original pizza is cut into, so that number is still 8. For dessert, they have a cake that is cut into 10 slices, so we can represent each slice as [ggfrac]1/10[/ggfrac]. If they eat 2 slices, that is [ggfrac]2/10[/ggfrac] of the cake. We can represent the whole cake as [ggfrac]10/10[/ggfrac]. To subtract [ggfrac]2/10[/ggfrac], find 10 - 2 = 8. They have [ggfrac]8/10[/ggfrac] of the cake left. Now you try: A pan of lasagna is cut into 12 equal pieces. If you eat 5 pieces, what fraction represents how much lasagna you have left?

Ski Trip It snowed 3[ggfrac]1/5[/ggfrac] inches yesterday and 5[ggfrac]3/5[/ggfrac] inches today. How much snow fell in all? Add 3[ggfrac]1/5[/ggfrac] + 5[ggfrac]3/5[/ggfrac] to find the total snowfall. First, add the whole numbers on their own. Then add the fractions on their own. Then combine the totals. 3 + 5 = 8 and [ggfrac]1/5[/ggfrac] + [ggfrac]3/5[/ggfrac]= [ggfrac]4/5[/ggfrac]. Together, that's 8[ggfrac]4/5[/ggfrac] inches of snow. Now you try: A recipe calls for 4[ggfrac]1/6[/ggfrac] cups of white flour and 2[ggfrac]3/6[/ggfrac] cups of whole wheat flour. How much flour do you need altogether?

Bobbing for Apples April and Marcos are bobbing for apples. It takes April 4[ggfrac]1/6[/ggfrac] seconds, and it takes Marcos 5[ggfrac]5/6[/ggfrac] seconds to get an apple. How much less time did April take than Marcos? We need to subtract 5[ggfrac]5/6[/ggfrac] - 4[ggfrac]1/6[/ggfrac] to find the difference. We can use the same method as for addition. First, subtract the whole numbers and then subtract the fractions. Finally, combine the totals. 5 - 4 = 1 and [ggfrac]5/6[/ggfrac] - [ggfrac]1/6[/ggfrac] = [ggfrac]4/6[/ggfrac]. April took 1[ggfrac]4/6[/ggfrac] seconds less than Marcos. Now you try: Yesterday, 4[ggfrac]1/8[/ggfrac] millimeters of rain fell, and today 6 [ggfrac]7/8[/ggfrac] millimeters of rain fell. How much more rain fell today than yesterday?

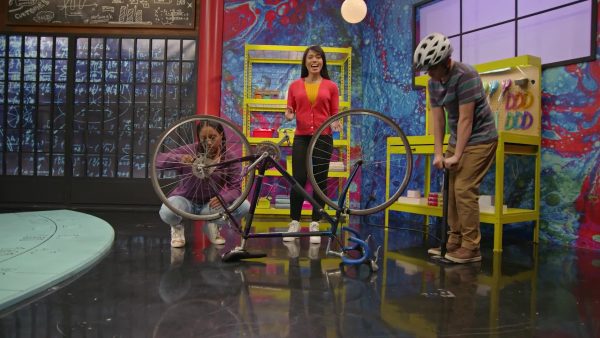
Bike Trip Marcos plans to bike to a store 2[ggfrac]3/5[/ggfrac] miles away, and then to a beach another 3[ggfrac]1/5[/ggfrac] miles away. How many miles will he bike in total, to get to the beach? We already know one method of adding mixed numbers, and now we learn another. We can turn each mixed number into a fraction. 2[ggfrac]3/5[/ggfrac] can be written as 1 + 1+[ggfrac]3/5[/ggfrac]. 1 = [ggfrac]5/5[/ggfrac], so this is the same as [ggfrac]5/5[/ggfrac] + [ggfrac]5/5[/ggfrac] + [ggfrac]3/5[/ggfrac], or [ggfrac]13/5[/ggfrac]. 3[ggfrac]1/5[/ggfrac] can be written as 1 + 1 + 1 + [ggfrac]1/5[/ggfrac], which is the same as [ggfrac]5/5[/ggfrac] + [ggfrac]5/5[/ggfrac] + [ggfrac]5/5[/ggfrac] + [ggfrac]1/5[/ggfrac], or [ggfrac]16/5[/ggfrac]. Now we find the total, [ggfrac]13/5[/ggfrac] + [ggfrac]16/5[/ggfrac] = [ggfrac]29/5[/ggfrac]. The last step is to write [ggfrac]29/5[/ggfrac] as a mixed number by simplifying:[ggfrac]29/5[/ggfrac] is the same as 5[ggfrac]4/5[/ggfrac]. Marcos will bike for 5[ggfrac]4/5[/ggfrac] miles to the beach. Now you try: 3[ggfrac]3/4[/ggfrac] + 2[ggfrac]2/4[/ggfrac] = ?

Baking A cake recipe calls for 4[ggfrac]3/4[/ggfrac] cups of chocolate chips in total, but 1[ggfrac]1/4[/ggfrac] cups should be set aside to put on top of the cake at the end. How many cups of chocolate chips should we add to the batter? To find the answer, we subtract 4[ggfrac]3/4[/ggfrac] - 1[ggfrac]1/4[/ggfrac]. 4[ggfrac]3/4[/ggfrac] is the same as 1 + 1 + 1 + 1 + [ggfrac]3/4[/ggfrac], or [ggfrac]4/4[/ggfrac] + [ggfrac]4/4[/ggfrac] + [ggfrac]4/4[/ggfrac] + [ggfrac]4/4[/ggfrac] + [ggfrac]3/4[/ggfrac] = [ggfrac]19/4[/ggfrac]. 1[ggfrac]1/4[/ggfrac] is the same as 1 + [ggfrac]1/4[/ggfrac] or [ggfrac]4/4[/ggfrac] +[ggfrac]1/4[/ggfrac] = [ggfrac]5/4[/ggfrac]. Now we can subtract the improper fractions: [ggfrac]19/4[/ggfrac] - [ggfrac]5/4[/ggfrac] = [ggfrac]14/4[/ggfrac]. Finally, convert [ggfrac]14/4[/ggfrac] into a mixed number: 3[ggfrac]2/4[/ggfrac]. Now you try: You have 6[ggfrac]2/5[/ggfrac] balls of yarn, and you need 4[ggfrac]3/5[/ggfrac] balls of yarn to knit a sweater. How many balls of yarn will you have left over?