Read About Ratios

A ratio shows a relationship between two amounts. A bunny has 2 eyes and 1 nose. That’s a ratio of 2 to 1. You can also write it as 2 : 1. If there are two bunnies, the ratio of eyes to noses becomes 4 to 2, or 4 : 2. For three bunnies, the ratio is 6 to 3, or 6 : 3, and for four bunnies, the ratio is 8 to 4, or 8 : 4. Like with equivalent fractions, you can multiply both numbers in a ratio to get another, equivalent ratio. Multiply 2 : 1 by 3 to get 6 : 3, or 6 eyes on 3 bunnies. Try this one yourself: A sign has 5 parts red for every 1 part white. With the same color ratio, a larger sign has 20 parts red. How many parts white does the larger sign have?

Part-to-whole ratios are related to fractions. A pack of 5 markers contains 1 blue marker. This is a part-to-whole ratio. We can represent part-to-whole ratios with fractions. Write this ratio as [ggfrac]1/5[/ggfrac]. We can use equivalent fractions to represent the number of blue markers in more packs. Two packs of markers have 2 blue markers out of 10 total, or [ggfrac]2/10[/ggfrac]. This is the same as multiplying the original numerator, 1, by 2 and multiplying the original denominator, 5, by 2. Try this one yourself: Find the part-to-whole ratio that describes the number of blue markers in 10 packs of markers.

Part-to-part ratios don’t show the whole. A fish tank contains 20 fish: 14 blue and 6 yellow. The ratio [ggfrac]14/20[/ggfrac] describes the number of blue fish out of the total. The ratio [ggfrac]6/20[/ggfrac] describes the number of yellow fish out of the total. These are both part-to-whole ratios. You can also use 'part-to-part' ratios to show this information. The ratio 14 : 6 compares the number of blue fish to the number of yellow fish. Similarly, the ratio 6 : 14 compares the number of yellow fish to the number of blue fish. Try this one yourself: A bag of marbles has 8 red marbles out of 15 total. The marbles that aren’t red are purple. Find the part-to-part ratio that compares the number of red marbles to the number of purple marbles. Then find the part-to-part ratio that compares the number of purple marbles to the number of red marbles.

You can simplify ratios by scaling them down. Simplifying ratios can make the comparisons easier to understand. Let’s say a local animal shelter has 24 dogs and 16 cats, or 24 : 16. You can divide both numbers by the same divisor to find an equivalent ratio. Divide by 2 to get 12 : 8. Divide by 2 again to get 6 : 4. Divide by 2 one more time to get 3 : 2. You could also divide 24 : 16 by 8 to get 3 : 2. Try this one yourself: Simplify the ratio “100 parakeets to 75 hamsters.”

Ratios can help you find the best deal. Emily saw a deal online, where 4 t-shirts cost $20. Amari saw another deal advertising the same t-shirts, where 8 t-shirts cost $32. You can use ratios to decide which deal is better. Emily can describe her ratio as “$20 to 4 shirts.” Dividing each of these numbers by 4, that is equivalent to $5 : 1 shirt. Amari can describe his deal as “$32 to 8 shirts.” Dividing each of these numbers by 8, that is equivalent to $4 : 1 shirt. Buying shirts with Amari’s deal saves $1 for each shirt, so it is the better deal. Try this one yourself:Which is the better deal: 5 pairs of socks for $15, or 2 pairs of socks for $12?

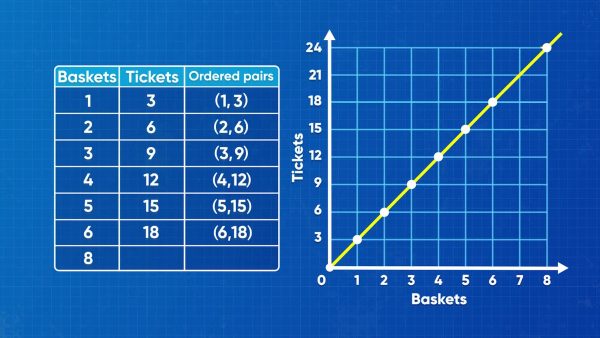
Graphing ratios shows patterns more visually. A carnival game involves a basketball hoop. For each basket you make, you win 3 tickets. This is a ratio of 3 : 1. You can use multiplication to make a set of equivalent ratios: 6 : 2, 9 : 3, 12 : 4, 15 : 5. These ratios can be displayed on a coordinate grid. The number of baskets goes on the x-axis, and the number of tickets goes on the y-axis. Then the ratios also represent coordinate pairs: (3, 1), (6, 2), (9, 3), (12, 4), (15, 5). Each point is 3 right and 1 up from the previous point. To predict the number of tickets more easily, draw a straight line through these points and keep going up and to the right. Try this one yourself:To get into a carnival, each child admission ticket is $5. Graph the cost of 1, 2, 3, 4, and 5 admission tickets on a coordinate grid. Draw a line through these points to find the cost of 8 admission tickets.

Many careers use ratios. Chefs use ratios to calculate the right amount of ingredients to use in a recipe. Florists use ratios to determine how many flowers are needed in each arrangement at a banquet. One of the responsibilities of a doctor is prescribing medication. Doctors often use ratios based on body weight to determine the proper dosages their patients should take.