You have already learned how to find surface area by unfolding 3D shapes into 2D shapes and adding up the areas of all their parts. In this lesson, you learn how to use variables to label the sides in a shape and find surface area more efficiently by using formulas.
To better understand surface area (using formulas)…
LET’S BREAK IT DOWN!
Surface Area of a Cube
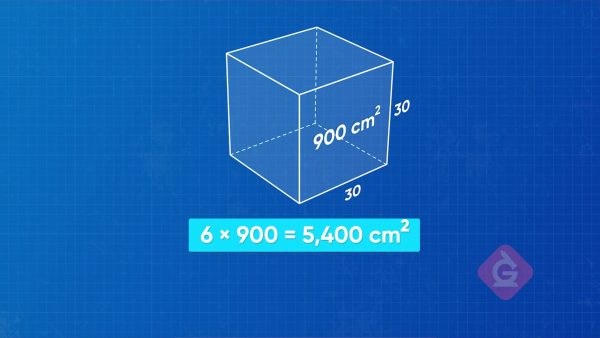
A cube is a rectangular prism that has 6 identical faces, and each face is a square. Since all sides have the same length, and all the faces have the same area, we can find the area of one face and multiply by 6 to find the surface area! If we let a be the length of the sides, then we can use the formula 6a2 to find the surface area of any cube. Now you try: What is the area of a cube with side length 4 cm?
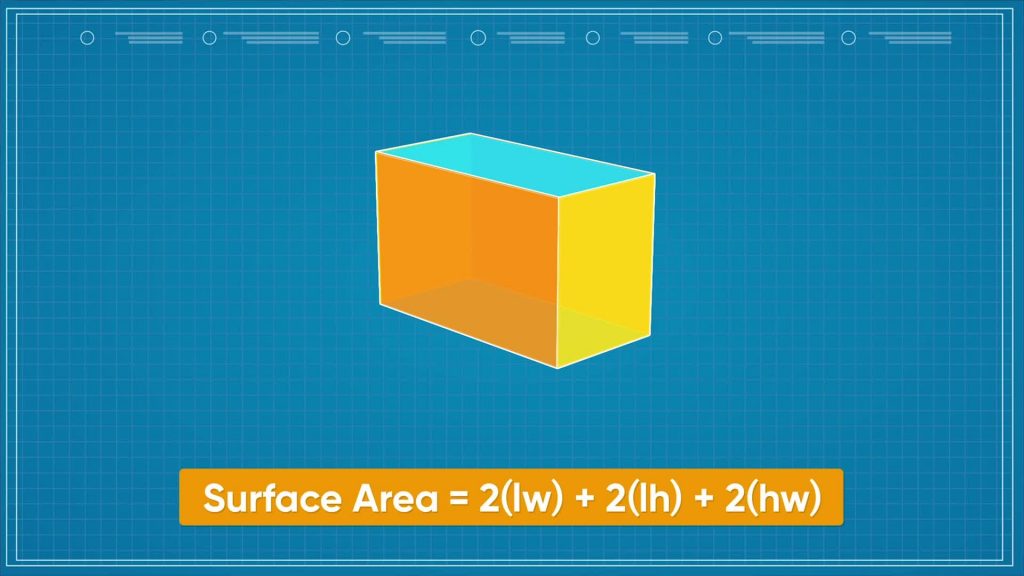
Surface Area of a Rectangular Prism
A rectangular prism is made up of 6 faces. In a rectangular prism, we have a length, a width, and a height, and we will call them l,w, and h. Since opposite faces have the same dimensions, we only need to find the areas of the 3 different faces, multiply each area by 2, and add the totals together to find the surface area. Then the surface area of a rectangular prism is 2l×w+2w×h+2(l×h). Now you try: Find the surface area of a rectangular prism that has length 6 m, width 3 m, and height 2 m.
Surface Area of a Triangular Prism
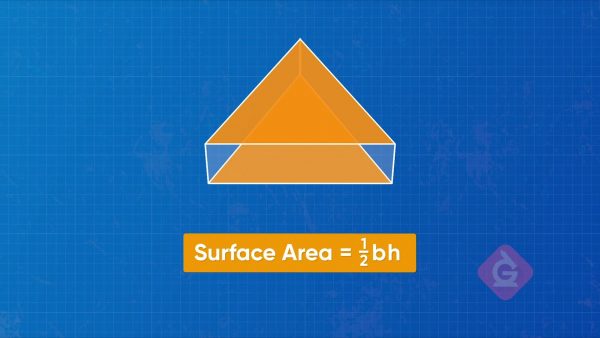
A triangular prism has a total of 5 faces: 2 triangular faces that are opposite each other and are the same, and 3 rectangular faces. We can find the area of one of the triangular faces, multiply it by 2, and then add the area of each of the rectangular faces. Then the formula for the surface area of a triangular prism is 2 x [ggfrac]b×h/2[/ggfrac] 2×b × h2+l×a+l×b+l×c which we can also simplify to b×h+l×a+l×b+l×c. It is important to remember that the width might be different for each of the 3 rectangles. Now you try: Find the surface area of a triangular prism where the triangular faces are triangles with side lengths 3 in., 4 in., and 5 in. The triangle base is 3 in. and its height is 4 in., and the rectangular faces have length 2 in.
Surface Area of a Cylinder
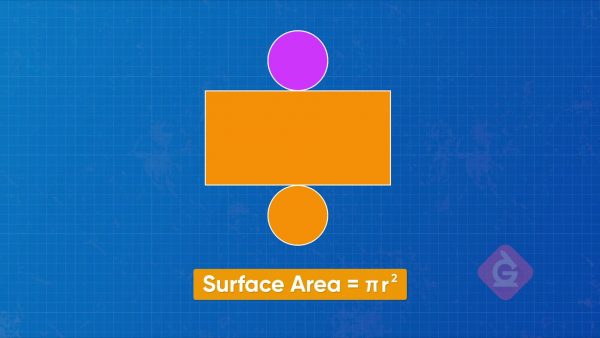
A cylinder is like a tube with a circular cap on each end. If we unravel it into a 2D shape, we get one long rectangle and two identical circles. Notice that as we unravel the cylinder, the circumference of the circle turns out to be the length of the rectangle! The other dimension of the rectangle is the height of the cylinder. Then the surface area of a cylinder is 2 times the area of a circle, plus the area of the rectangle. Now you try: Find the surface area of a cylinder that has radius 3 mm and height 6 mm. Use 3.14 for pi and round to the nearest tenth.
Surface Area of a Cone
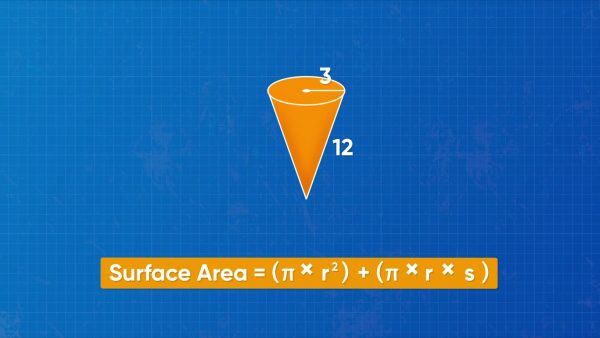
Cones are shaped like ice cream cones with a circular lid that covers the opening at the top. An unrolled cone looks like a part of a circle, and the lid is a circle. The unrolled cone can be decomposed into a rectangle that has side lengths πr and s, where s is the slant height of the cone. To find the surface area, we can find the area of the rectangle and add it to the area of the circular lid. Then the formula for surface area of a cone is πr2 + πrs. Now you try: What is the surface area of a cone with radius 4 feet and slant height 7 feet?
SURFACE AREA (USING FORMULAS) VOCABULARY
SURFACE AREA (USING FORMULAS) DISCUSSION QUESTIONS
The formula for the surface area of a cube is 6s2. If a side of the cube measures 3 m, how can you find the surface area of the whole cube?
Can you use the formula for the surface area of a rectangular prism to find the surface area of a cube?
To calculate the surface area of a cylinder, do you need to use πr2 or πr?
How should you label a right triangular pyramid so that you can use the surface area formula b×h+a×d+b×d+c×d?
The formula for the surface area of a cone uses slant height. What is that?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial





