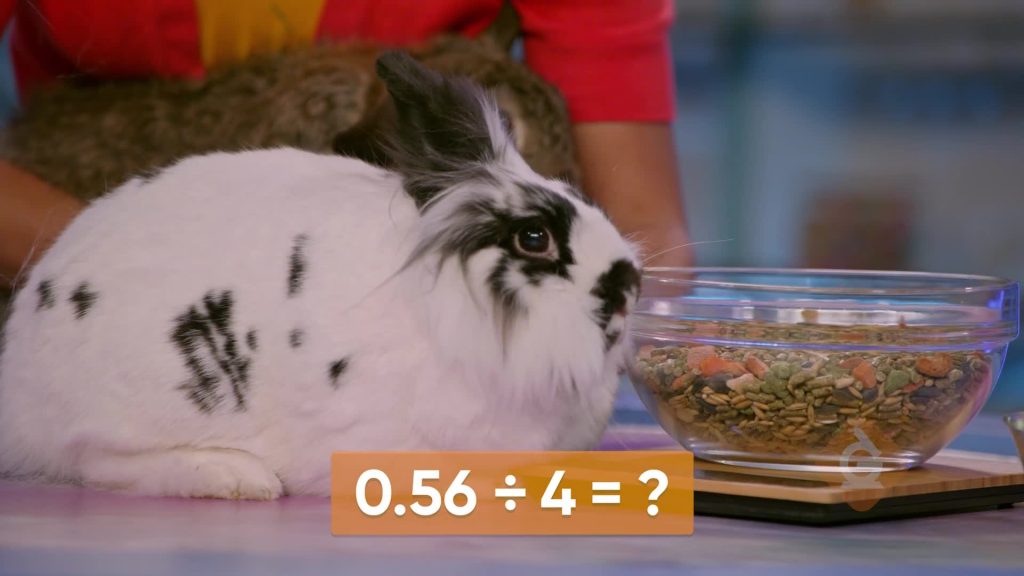
You can solve problems with decimals exactly the way you solved problems with whole numbers. Use keywords to identify if you need to add, subtract, multiply, or divide to solve.
To better understand solving problems with decimals…
LET’S BREAK IT DOWN!
Hiking

Adesina, April, and Marcos hiked all day. They need to add up the distances they hiked to find out how far they traveled in all. The first trail was 1.7 kilometers long. The second trail was 3.2 kilometers long. To find out how much they hiked altogether, add 1.7 + 3.2. To do this, use models that represent whole and decimal numbers. We can represent 3.2 as 3 wholes and 2 tenths. We can represent 1.7 as 1 whole and 7 tenths. To add, group the wholes and group the tenths. 3 wholes plus 1 whole is 4 whole kilometers. 7 tenths plus 2 tenths is 9 tenths of a kilometer. Then we have 4 wholes and 9 tenths, or 4.9 kilometers. This means that they hiked 4.9 kilometers altogether. To check the answer, round the starting numbers to the nearest whole. 3.2 can be rounded to 3 and 1.7 can be rounded to 2. Add 3 and 2 to get 5. 5 is close to 4.9, so the answer is reasonable. Numbers with hundredths can be added the same way. If Marcos bought an energy bar for $2.34 and April bought trail mix for $1.89, how much money did they spend in all? 2.34 can be represented as 2 wholes, 3 tenths, and 4 hundredths. 1.89 can be represented as 1 whole, 8 tenths, and 9 hundredths. Adding them together, we have 3 wholes, 11 tenths, and 13 hundredths. Because we have more than 9 hundredths and tenths, we have to regroup some numbers. 10 hundredths can be regrouped to make 1 tenth, so 13 hundredths is 1 tenth and 3 hundredths. Then we have 12 tenths in total. 10 tenths can be regrouped to become 1 whole, so 12 tenths is 1 whole and 2 tenths. Altogether there are 4 wholes, 2 tenths, and 3 hundredths, or $4.23. Now you try: Add 4.58 + 2.39.
Science Project

Marcos, April, and Adesina grew crystals for a science project. Marcos’s crystal weighs 5.6 grams, and April’s weighs 3.5 grams. How much more does Marcos’ crystal weigh than April's? We can use decimal square models to find the answer. To find the difference, we always start with the bigger number, and we can represent 5.6 using 5 wholes and 6 tenths. To subtract, we need to take away 3.5, or 3 wholes and 5 tenths. 5 – 3 = 2 wholes. 6 tenths – 5 tenths = 1 tenth. We have 2 wholes and 1 tenth, or 2.1, remaining. Marcos’ crystal weighs 2.1 more grams than April’s. Estimate the difference to check the answer. Round 5.6 to 6 and 3.5 to 4. 6 – 4 = 2. 2 is close to 2.1, so the answer is reasonable. April’s crystal display cost $3.59. Marcos’ display cost $1.95. How much more did April’s display cost than Marcos's? Find 3.59 – 1.95 to find the difference. Use the decimal square model to show the larger number. 3.59 is 3 wholes, 5 tenths, and 9 hundredths. To subtract, cross out 1.95, or 1 whole, 9 tenths, and 5 hundredths in all. First, cross out 5 hundredths. There are 4 hundredths left. Next, we need to cross out 9 tenths, but there are only 5 tenths. Regroup 1 whole into 10 tenths. Now there are 2 wholes and 15 tenths. Subtract the 9 tenths. 15 – 9 = 6, so there are 6 tenths left. Lastly, subtract 1 whole from 2. We have 1 whole, 6 tenths, and 4 hundredths left. That means that April's display cost $1.64 more than Marcos's. Now you try: What is $6.72 – $3.45?
Stacking Shelves

Adesina stacks 4 drawers on top of each other. Each drawer is 0.3 meter tall. How tall is the stack? Find out by multiplying 4 by 0.3. Since multiplication is just repeated addition, 4 times 0.3 is the same as 0.3 + 0.3 + 0.3 + 0.3. Use decimal squares to model the addition. 0.3 means 3 parts out of 10. Show that 4 times. Next, count up all the tenths: there are 3, 6, 9, 12 tenths. To write this as a decimal, regroup 10 tenths to make 1 whole. That gives 1 whole and 2 tenths, or 1.2 meters. What if you stack 3 bigger shelves that are each 2.53 feet tall? To find the height of this stack, multiply 2.53 by 3. 2.53 can be modeled as 2 wholes, 5 tenths, and 3 hundredths. To multiply by 3, add each number of units 3 times. This gives 6 wholes, 15 tenths, and 9 hundredths in all. Regroup 15 tenths as 1 whole and 5 tenths. The answer is 7 wholes, 5 tenths, and 9 hundredths, or 7.59 meters tall. To use estimation to check the answer, round 2.53 to 3. 3 × 3 = 9, which is close to the answer. To multiply a decimal by a decimal, such as 0.7 times 0.3, use a model to show 0.3 as 3 parts out of 10. To show 7 tenths of 3 tenths, split each tenth into 10 equal parts, and then color only 7 of the parts in each tenth. When tenths are split into 10 parts each, there are 100 pieces in the whole. That means that each of those small squares represents one hundredth. Each model shows 7 hundredths. There are 3 models to show the original 3 tenths. So the answer is 21 hundredths, or 0.21. Now you try: Multiply 4 by 2.61 meters.
Pets

Adesina has a puppy and April and Marcos each have a rabbit. Adesina feeds her dog 3 times a day. She fed her dog 0.6 kg of food in one day. How much did she feed her dog for each meal? To find the answer, divide 0.6 by 3. Model 0.6 by showing 6 tenths, or 6 out of 10 parts of a whole. If 6 tenths is split into 3 equal groups, each group has 2 tenths in it. Then the answer is 0.2 kg. Marcos has 0.48 kg of rabbit food and needs to feed his rabbit 4 equal meals. To split 0.48 into 4 equal parts, show 0.48 as 4 tenths and 8 hundredths. If they are divided into 4 equal groups, each group contains 1 tenth and 2 hundredths, or 0.12 kg. Now you try: What is 0.72 kg divided by 6?
SOLVE PROBLEMS WITH DECIMALS (USING MODELS) VOCABULARY
SOLVE PROBLEMS WITH DECIMALS (USING MODELS) DISCUSSION QUESTIONS
If you are calculating 3.64 – 2.14, which number should you represent using the fraction square model? What is the second step?
You want to calculate 3.4 – 0.8. You represent 3.4 using 3 wholes and 4 tenths. What else do you need to do before you can subtract 8 tenths?
How can you use skip counting to multiply 6 × 1.4?
Mimi multiplies 4 by 2 wholes, 3 tenths, and 7 hundredths and gets 8 wholes, 12 tenths, and 28 hundredths. Is that the final answer?
What can you do to check if 3.8 × 5.1 = 19.38 makes sense?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial





