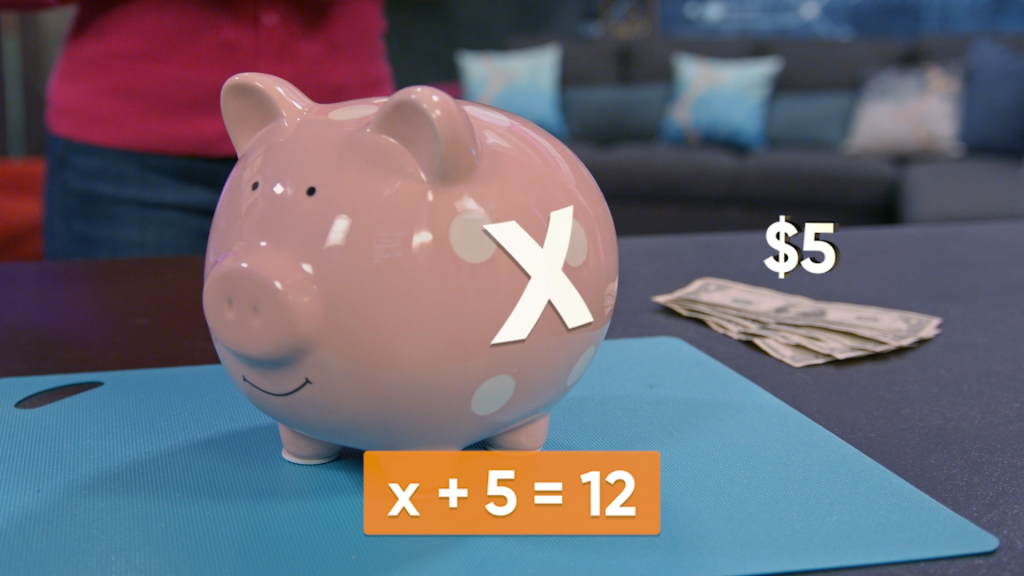
Algebraic equations are equations where one or more of the numbers in the equation are unknown. You can represent unknowns using variables, like x. When you solve an equation, you find a value of the variable that makes the equation true.
To better understand 1-step algebraic equations…
LET’S BREAK IT DOWN!
You can turn real-world problems into algebraic equations.
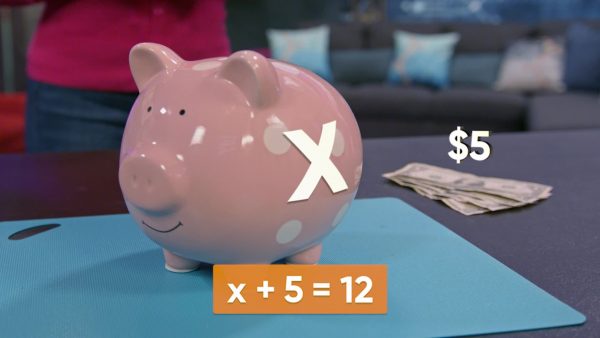
You have $5 in your piggy bank. You add some more money to the piggy bank. Now, the total amount in the bank is $12. You can write an algebraic equation to represent the problem. You know that 5 plus some more is 12 in all. Represent 'some more' with the variable x. The equation becomes 5 + x = 12. Now you try: You had $40, and you bought a shirt for an unknown amount of money. Now you have $16. Write an algebraic equation to represent the problem.
Solve algebraic equations that involve addition.

To solve the equation 5 + x = 12, you could try plugging in different values for x until the total equals 12, but that could take a while, especially if the numbers are greater. There is a more efficient method! Instead, you can use inverse operations. An equation connects two expressions of the same value with an equal sign. That means that if you apply an operation to one side of the equation, you need to do the same on the other side. If you don't, the sides are no longer equal! To keep them balanced, you always need to add or take away the same amount on both sides. To find the value of x, you need to get x all by itself on one side of the equation. You can apply inverse operations to isolate variables. The inverse operation to addition is subtraction. Since x has 5 added to it, you can subtract 5 to isolate. Make sure to subtract from both sides. 5 + x – 5 = 12 – 5. x = 7. You added $7 more to the piggy bank. You can substitute your solution into the original equation to check if it makes the equation true. 5 + 7 = 12. 12 = 12. It's true, so x = 7 is the solution. Now you try: Use inverse operations to solve x + 9 = 14
Solve equations that involve subtraction.

At the end of a bake sale, you have 42 cupcakes left. If you sold 9, how many did you have to start with? Represent the number of cupcakes at the start with the variable x. x – 9 = 42. The inverse operation of subtraction is addition. Add 9 to both sides. x – 9 + 9 = 42 + 9. x– 9 + 9 is equal to x. On the right side, 42 + 9 = 51. So x= 51. That means you started out with 51 cupcakes. Substitute the answer into the original equation to check: 51 – 9 = 42. 42 = 42. The solution is correct. Now you try: Use inverse operations to solve x – 17 = 3.
Solve equations that involve multiplication.

You have 3 fish tanks, each containing the same number of fish. Altogether, you have 36 fish. Let x represent the number of fish in each tank. 3 tanks of x fish is equal to 36 in total: 3x = 36. Since the inverse of multiplication is division, divide both sides by 3 to isolate x. [ggfrac]3x/3[/ggfrac]=[ggfrac]36/3[/ggfrac]. [ggfrac]3/3[/ggfrac]=1 and [ggfrac]36/3[/ggfrac]=12. So, x = 12. There are 12 fish in each tank. Substitute to check your answer. 3(12) = 36. 36 = 36. The equation is true, so the solution is correct. Now you try: Solve 5x = 75.
Solve equations that involve division.

You and your friends make money walking dogs. If you split all the money that you made equally between 7 people, and each person gets $9, how much money did you make in all? Let x represent the total amount of money made before it was shared. The equation is [ggfrac]x/7[/ggfrac]=9. The inverse of division is multiplication. Multiply both sides by 7. [ggfrac] 7∙x/7 [/ggfrac] =9∙7. [ggfrac]7/7[/ggfrac]=1 and 9∙7=63. So the equation simplifies to x = 63. Your group made $63 walking dogs. Substitute to check: [ggfrac]63/7[/ggfrac]=9. 9=9. The equation is true, so the solution is correct. Now you try: Solve [ggfrac]x/4[/ggfrac]=12.
SOLVE ALGEBRAIC EQUATIONS(1-STEP) VOCABULARY
SOLVE ALGEBRAIC EQUATIONS(1-STEP) DISCUSSION QUESTIONS
What is a variable? What does it look like in an equation?
x – 8 = 7 What operation is done to x, and what operation should you use to solve for x?
7x = 21 What operation is done to x, and what operation should you use to solve for x?
To solve [ggfrac]x/4[/ggfrac]=10, Joe’s first step was [ggfrac]4 ∙ x/4 ∙ 4[/ggfrac]=10∙4. What did Joe do wrong?
Morgan says that the solution to the equation 4x = 20 is x = 6. Can you check if she is right?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial






