
A pattern is a set of shapes or numbers that change based on a rule. A pattern could be repeating, like ABABAB, or continue on, like ABCDEFG.
To better understand generating a pattern of shapes or numbers…
LET’S BREAK IT DOWN!
Shape Patterns

April's bracelet is made of parts that are circles and triangles. The bracelet has a pattern: circle, triangle, circle, triangle, … This is an example of a repeating pattern. Since the shapes take turns being next, you can predict that the next shape is another circle! A repeating pattern uses a rule that repeats over and over. A pattern is something that repeats in a predictable way. The slightly more challenging pattern could be: circle, circle, pentagon, circle, circle, pentagon, circle, circle, pentagon. In this example, the rule is you have two circles, and then a pentagon. Then that pattern of three shapes repeats. You can predict the next shapes, two circles and a pentagon! Another pattern is: triangle, square, pentagon, hexagon. This one is harder because none of the shapes are repeating. Think about the properties of these shapes. Each shape has one more side than the shape before it! Hexagons have 6 sides, so the next shape would have 7 sides, a heptagon. Try this one yourself: Draw a new shape pattern. Trade patterns with a partner. Identify your partner's pattern.
Addition Examples

Lists of numbers can also show patterns, not just shapes. Let's say a dish has 3 raisins. The next dish has 6 raisins. Then there are 9, 12, 15, and 18 raisins in the next dishes. What pattern can you find? The number of raisins in each dish increases by 3. You add 3 to get the next number. 18 + 3 = 21. So the next dish has 21 raisins. Continue the pattern to get 24, 27, and 30 raisins. It’s kind of like predicting the future! There is a second pattern you can also use here: 3 is odd, 6 is even, 9 is odd, 12 is even, and so on. That is because an even number plus an odd number is an odd number, and an odd number plus an odd number is an even number. So, the pattern goes back and forth between odd and even. Here is another example. Sports drinks come in packs of 6. What pattern do six of these packs form? The total number of sports drinks is: 6, 12, 18, 24, 30, 36. The rule is: add 6 for each new pack of drinks. These numbers are all even, because we started with 6 (an even number) and we add 6 (an even number) each time. That is, adding two even numbers results in another even number. The numbers in this list are all twice as much as the numbers in the raisins list. One dish had 3 raisins, and we added threes. One pack has 6 sports drinks, and we add sixes. Try this one yourself: Write three new number patterns: one where the numbers are all even, one where some numbers are even and others are odd, and one where the numbers are all odd.
Fuel Gauge

Some patterns have numbers that slowly go down, like the fuel gauge on a car’s dashboard. One car's gauge starts at 20 liters in the gas tank, then goes down to 18, 16, 14, 12, 10, and 8. This makes sense because you use gas as you drive, so there’s less and less gas left in the tank. This is an example of a decreasing number pattern, where each new number is less than the previous one. In this case, the rule is subtract 2. This pattern continues until the gauge shows 0, which means there’s no more gas left in the tank. Try this one yourself: Think of a new real-world situation that has a decreasing number pattern. Does the pattern end or go on forever? Try to convince someone else that you’re correct.
Bacteria
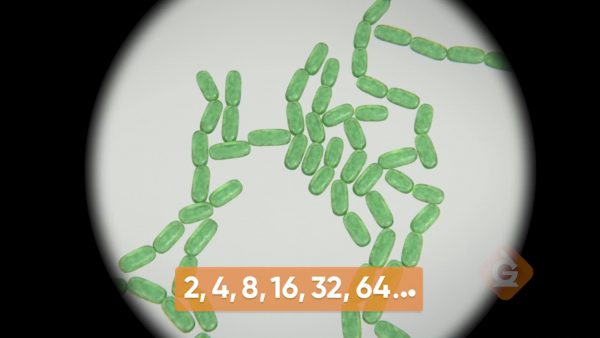
Scientists use number patterns to study bacteria and how it grows. After only 10 minutes, 2 bacteria split into 4. After 10 more minutes, the 4 split into 8. 10 minutes later, they split to 16! Then there are 32, and eventually 64 bacteria. In this instance, addition just doesn’t work. There’s a new kind of rule: multiply by 2. You can predict that the number of bacteria in another 10 minutes is 64 × 2 = 128. These are all even numbers, because multiplying an even number by an even number always gives you an even number. A pattern that’s related to this, but a little different, is: 243, 81, 27, 9, 3. This is a decreasing pattern, but subtraction doesn’t do the trick. Notice that 3 × 3 = 9, 9 × 3 = 27, 27 × 3 = 81, and 81 × 3 =243. The rule must be the opposite of multiplying by 3: dividing by 3! The next number is 1. Try this one yourself: Write a multiplication pattern and a division pattern. Trade patterns with a partner. Figure out the next three numbers of your partner's pattern.
GENERATE NUMBER PATTERNS (SEQUENCES THAT FOLLOW A GIVEN RULE) VOCABULARY
GENERATE NUMBER PATTERNS (SEQUENCES THAT FOLLOW A GIVEN RULE) DISCUSSION QUESTIONS
What advice would you give a student who was absent today about how to figure out shape patterns?
Give an example of an “increasing” and a “decreasing” number pattern. Explain the rule for each pattern.
Give examples of a rule that makes a multiplication pattern and a rule that makes a division pattern. Explain the rule for each pattern.
How is the rule “double” different from the rule “double plus 10”?
Give an example of a rule that goes on forever, and a rule that doesn’t.
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial






