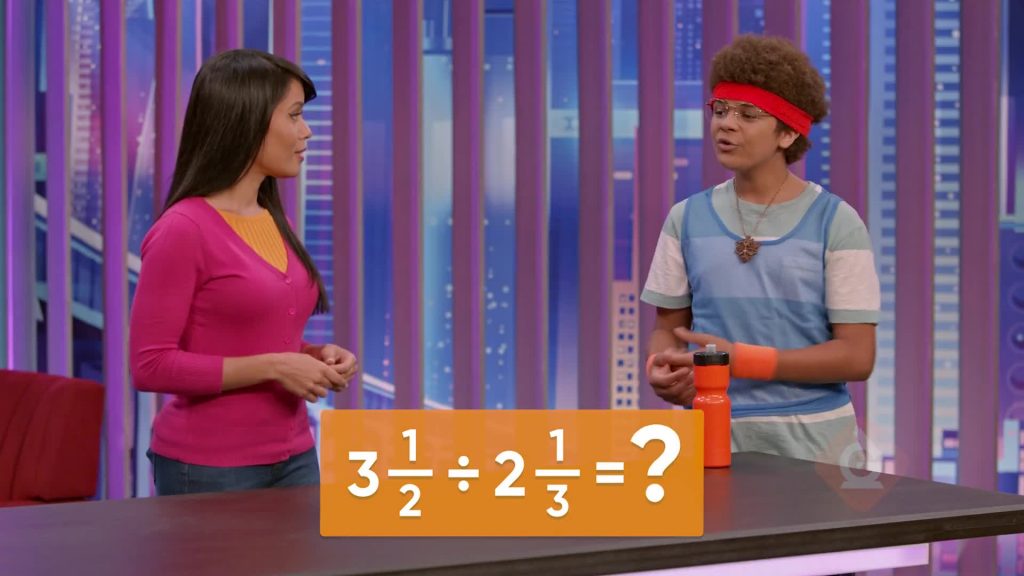
Previously, you learned how to divide a whole number by a fraction and a fraction by a whole number. Today you learn that the same processes you already know can help you divide fractions by fractions.
To better understand dividing fractions by fractions…
LET’S BREAK IT DOWN!
Divide 5 by [ggfrac]1/4[/ggfrac]
![Divide 5 by [ggfrac]1/4[/ggfrac]](https://www.generationgenius.com/wp-content/uploads/2021/08/Ep613-Gr6_Dividing-Fractions-by-Fractions-READING1-600x338.jpg)
Imagine we serve 5 quesadillas at a party, and each one of them is cut into fourths. To find out how many pieces we have in total, we need to divide 5 by [ggfrac]1/4[/ggfrac]. If we draw 5 circles and split each of them into 4 equal parts, we have a total of 20 pieces. We can rewrite division problems as multiplication problems: We keep the first number the same, we change the operation to multiplication, and we flip fraction so [ggfrac]1/4[/ggfrac] becomes 4. Then 5 ÷ [ggfrac]1/4[/ggfrac] is the same as 5 x 4, which is 20! Now you try: Solve 3 ÷ [ggfrac]1/5[/ggfrac].
Divide 3 by [ggfrac]3/4[/ggfrac]
![Divide 3 by [ggfrac]3/4[/ggfrac]](https://www.generationgenius.com/wp-content/uploads/2021/08/Ep613-Gr6_Dividing-Fractions-by-Fractions-READING2-600x338.jpg)
To solve 3 ÷ [ggfrac]3/4[/ggfrac], we follow the keep-change-flip method again to turn the division problem into a multiplication problem: We keep the 3, we change the operation to multiplication, and we flip the fraction. Then 3 ÷ [ggfrac]3/4[/ggfrac] becomes 3 x [ggfrac]4/3[/ggfrac] which is equal to [ggfrac]12/3[/ggfrac], which simplifies to 4! Now you try: Solve 4 ÷ [ggfrac]2/3[/ggfrac].
Dividing Fractions by Fractions

A community garden is [ggfrac]3/4[/ggfrac] of an acre, and we want to divide it into sections that are [ggfrac]1/8[/ggfrac] of an acre. How many sections are there? We can solve this by dividing [ggfrac]3/4[/ggfrac] ÷ [ggfrac]1/8[/ggfrac]. Even though we are dividing a fraction by a fraction, we can still use the keep-change-flip method. We keep [ggfrac]3/4[/ggfrac], we change the operation to multiplication, and we flip [ggfrac]1/8[/ggfrac] so that it becomes [ggfrac]8/1[/ggfrac]. Now the problem is the same as [ggfrac]3/4[/ggfrac] x [ggfrac]8/1[/ggfrac]. Remember that when we multiply fractions, we multiply the numerator by the numerator, and the denominator by the denominator. 3×8=24 and 4×1=4. So our answer is [ggfrac]24/4[/ggfrac], which simplifies to 6! The garden has 6 sections. Now you try: Solve [ggfrac]4/6[/ggfrac] ÷ [ggfrac]1/3[/ggfrac].
Quotients That Are Mixed Numbers

You have [ggfrac]5/6[/ggfrac] yard of fabric that you want to make shirts out of. Each shirt needs [ggfrac]2/5[/ggfrac] yard of fabric. How many shirts can you make? We can find out by solving [ggfrac]5/6[/ggfrac] ÷ [ggfrac]2/5[/ggfrac]. If we use the keep-change-flip method, we can turn this into the multiplication problem [ggfrac]5/6[/ggfrac] x [ggfrac]5/2[/ggfrac], which is equal to [ggfrac]25/12[/ggfrac]. Since 25 is greater than 12, we know that this fraction is greater than one whole. 25 divided by 12 is 2 with a remainder of 1, so this is equal to 2[ggfrac]1/12[/ggfrac]. That means we can make 2 shirts, and we will have a little bit of fabric left over. Now you try: Solve [ggfrac]8/5[/ggfrac] ÷ [ggfrac]1/3[/ggfrac].
Dividing Using Mixed Numbers

If you run a total of 2[ggfrac]3/4[/ggfrac] miles on a track and each lap is [ggfrac]11/12[/ggfrac] mile, how many laps did you run? We can find out by solving 2[ggfrac]3/4[/ggfrac] ÷ [ggfrac]11/12[/ggfrac]. First, we need to convert the mixed number into a fraction that is greater than 1. We want to express the whole number 2 using the denominator 4. 2 = [ggfrac]4/4[/ggfrac] + [ggfrac]4/4[/ggfrac] = [ggfrac]8/4[/ggfrac], plus [ggfrac]3/4[/ggfrac] equals [ggfrac]11/4[/ggfrac] in total. Now we have [ggfrac]11/4[/ggfrac] ÷ [ggfrac]11/12[/ggfrac] and we can use the keep-change-flip method to rewrite the problem as [ggfrac]11/4[/ggfrac] x [ggfrac]12/11[/ggfrac]. This is equal to [ggfrac]132/44[/ggfrac], which simplifies to 3! You ran 3 laps on the track. Now you try: Solve 1[ggfrac]2/6[/ggfrac] ÷ [ggfrac]2/3[/ggfrac].
DIVIDING FRACTIONS BY FRACTIONS VOCABULARY
DIVIDING FRACTIONS BY FRACTIONS DISCUSSION QUESTIONS
How can you turn [ggfrac]3/4[/ggfrac] ÷ [ggfrac]1/2[/ggfrac] into a multiplication problem?
To turn a division problem into a multiplication problem, could you instead flip the first fraction?
Is [ggfrac]3/4[/ggfrac] ÷ [ggfrac]1/2[/ggfrac] the same as [ggfrac]1/2[/ggfrac] ÷ [ggfrac]3/4[/ggfrac]? Explain why or why not.
What is the first thing you should do to divide [ggfrac]1/2[/ggfrac] ÷ 1[ggfrac]3/5[/ggfrac]?
If you solve [ggfrac]1/2[/ggfrac] ÷ 1[ggfrac]3/5[/ggfrac], should the answer be less than or greater than [ggfrac]1/2[/ggfrac]?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial





