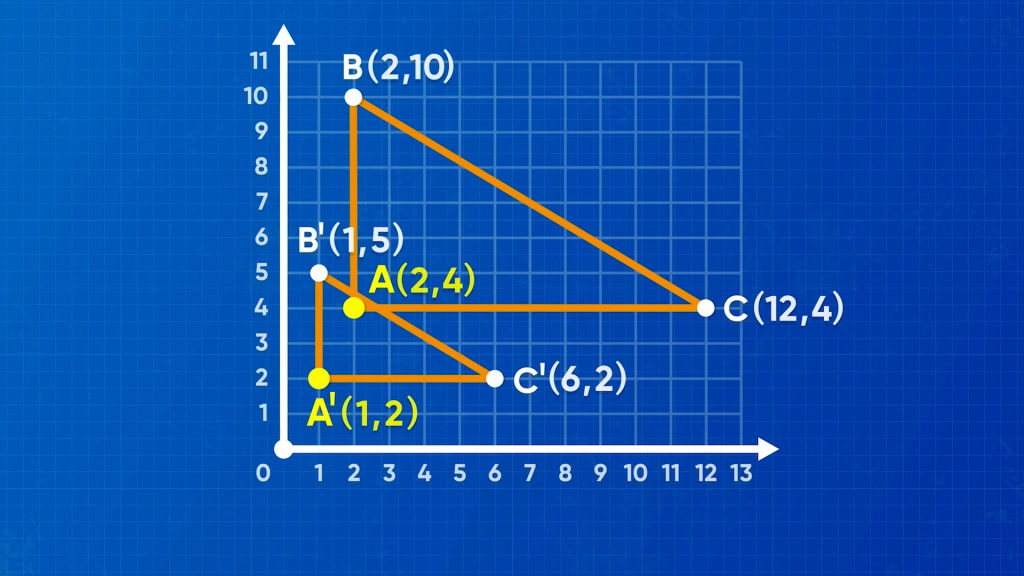
Just like you can translate and reflect shapes on a coordinate plane, you can also rotate and dilate them. When you rotate a shape, the resulting shape is congruent to the original. When you dilate a shape, the resulting shape is similar to the original.
To better understand translations: rotations & dilations…
LET’S BREAK IT DOWN!
Plot values on a coordinate plane.
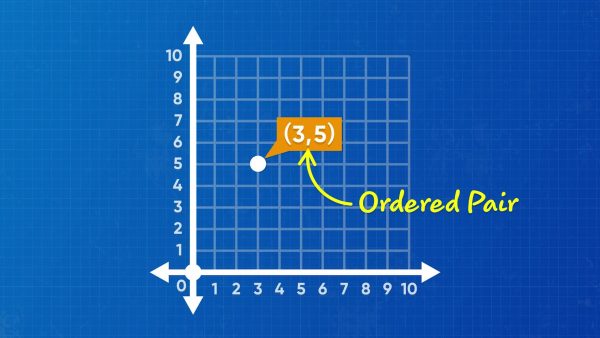
All points on a coordinate plane can be described using an ordered pair where the first number is x and the second is y. An ordered pair is written (x, y). The values for x and y tell you how far the point is away from the origin on each of the two axes. For example, the point (3, 5) is 3 units to the right of the origin and 5 units above the origin. The point (3, –5) is three units to the right and 5 units down from the origin. Try this yourself: Place the following points on a coordinate plane, (3, 7), (3, –7), (5, 6), (–5, 6).
What is dilation?
A dilation is a type of transformation where you make something larger or smaller. In a dilation on a coordinate plane, a point, set of points, or figure is expanded or contracted relative to the origin. We can make a dilation by multiplying both coordinates of each point by the same number. The number we multiply by to make a dilation is called a scale factor. We can break “scale factor” down to remember what it means: “scale,” tells us how big or small something is, and “factor” is something you multiply by in a multiplication sentence. So, a scale factor is a number to multiply by to change the size of something. In a dilation, there are two figures. The first figure is called the preimage, and the second figure (which we get from performing the dilation) is called the image. If we multiply the original by a scale factor larger than 1, we perform an enlargement. If the scale factor is less than 1, we perform a reduction. Try this yourself: A preimage is dilated by a factor of 0.3. Is the dilation an enlargement or a reduction?
Dilate a shape.
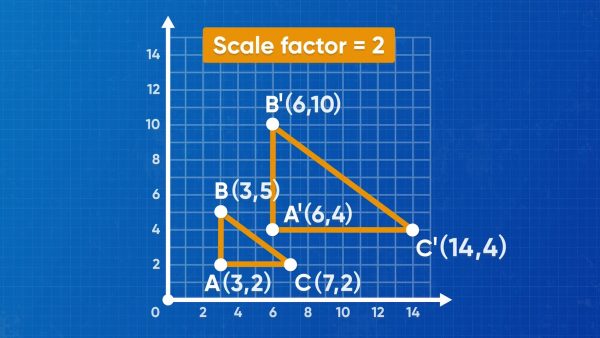
In enlargement, the points in a figure move farther away from the origin, and the side lengths of the figure increase. In a reduction, the points of the figure move closer to the origin, and the side lengths in the figure decrease. For example, if we dilate the point (4, 6) by a scale factor of 2, the resulting image point is (4 × 2, 6 × 2) = (8, 12). If we dilate that same point by a scale factor of [ggfrac]1/2[/ggfrac], the resulting image point is (4 × [ggfrac]1/2[/ggfrac], 6 × [ggfrac]1/2[/ggfrac]) = (2, 3). Try this yourself: Choose three different scale factors and dilate the point (4, –8) by each of them. What do you notice?
What is rotation?

Rotations are transformations where points and figures are turned on a coordinate plane. Many rotations are about the origin. In this context, “about” means around. When rotating a point about the origin, imagine a line connecting the origin to the point, and then rotate the line clockwise by the correct angle of rotation. While rotating, the length of the line between the origin and the point stays the same. If a pencil traced the path of the point around one full rotation, it would draw a circle. The common rotations are quarter turns of the circle. Since there are 360° in a circle, one-quarter turn is 90°. Try this yourself: How many degrees are there in a half turn?
Rotate a shape.
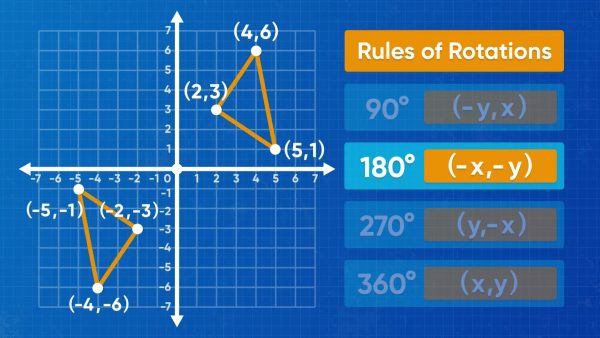
You can use mapping rules to summarize the coordinates of the image points following a rotation. The mapping rule shows what the original point is, and what that point becomes to produce the image. For example, a point (x, y) undergoing a 90° clockwise rotation becomes (y, –x). Written as a mapping rule, we use an arrow to mean “becomes” or “goes to” or “maps to,” so the mapping rule for this rotation is (x,y)→(y,-x). Let’s use this rule to rotate (3, 2) 90° clockwise. First, we know that the mapping rule is (x,y)→(y,-x), so we substitute the values for x and y into the rule to get the answer (3, 2)→(2,-3). This means that the image point is (2, –3). The mapping rule for a 180° clockwise rotation is (x,y)→(-x,-y), and a 270° rotation is (x,y)→(-y,x). Since a 360° rotation is a full turn, the image and original are the same. Try this yourself: Find the image of the point (6, 4) following a 90°, 180°, 270°, and 360° clockwise rotation.
TRANSFORMATIONS: ROTATIONS & DILATIONS VOCABULARY
TRANSFORMATIONS: ROTATIONS & DILATIONS DISCUSSION QUESTIONS
What is a scale factor?
What is the difference between an enlargement and a reduction?
How do you rotate a figure 90°?
How can you determine what transformation was used to create an image?
What does it mean for two 2D figures to be similar?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial
We use cookies to make your experience with this site better. By using this site you agree to our use of cookies. Click "Decline" to delete and block any non-essential cookies for this site on this specific property, device, and browser. Please read our privacy policy for more information on the cookies we use.Learn More
We use cookies to improve your experience. By using this site, you agree to our use of cookies. Click "Decline" to block non-essential cookies. See our privacy policy for details.Learn More





