Read About Surface Area Using Nets (Prisms & Pyramids)

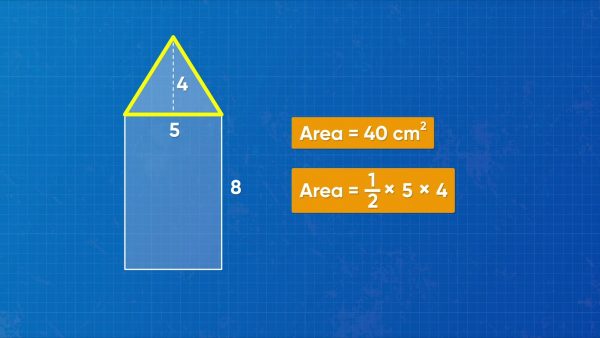
Find the area of a composite shape. The area of a complex shape can be found by breaking a shape into simpler shapes. You have a picture of an arrow pointing to the right. The arrow consists of a rectangle and a triangle. The rectangle is 8 centimeters by 5 centimeters, so its area is 8×5=40 square centimeters. The triangle has base 5 centimeters height 4 centimeters. So, the area of the triangular section is [ggfrac]1/2[/ggfrac](5)(4) =10 square centimeters. The total area of the arrow is 40+10=50 square centimeters. Try this one yourself: What is the area, in square centimeters, of a triangle with base 5 centimeters and height 12 centimeters?

Find the surface area of a barn owl box. Surface area is the total area of the faces of a 3D solid. You're building a barn owl box to help barn owls sleep during the day. You want to cover the box with paper to help it blend in outside. The amount of paper needed is the same as the surface area of the box. Since the box is a rectangular prism, its net has 6 rectangles. The box measures 3 units by 4 units by 2 units. Two faces measure 3-by-4, so they each have area 3×4=12 square units. Two faces measure 4-by-2, so they each have area 4×2=8 square units. Two faces measure 3-by-2, so they each have area 3×2=6 square units. The surface area is the sum: 12+12+8+8+6+6=52 square units. That means you need 52 square units of paper to cover the box. Try this one yourself: A rectangular prism measures 5 centimeters by 10 centimeters by 8 centimeters. What is the surface area, in square centimeters, of the prism?

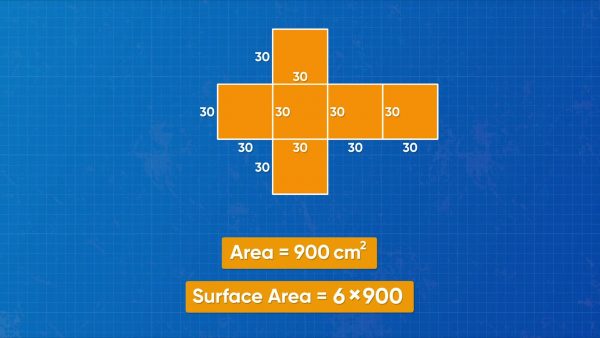
Find the surface area of a fish tank. You have a fish tank shaped like a cube. Every edge of the fish tank measures 30 centimeters. What is the surface area of the tank? In a cube, all 6 faces are the same size of square. The area of each square is 30×30=900 square centimeters. Since all the other squares have the same dimensions, the surface area of the cube is 900+900+900+900+900+900, or 900×6=5,400 square centimeters. The surface area of the fish tank is 5,400 square centimeters. Try this one yourself: A large cube has edges that each measure 2 meters. What is the surface area, in square meters, of the cube?

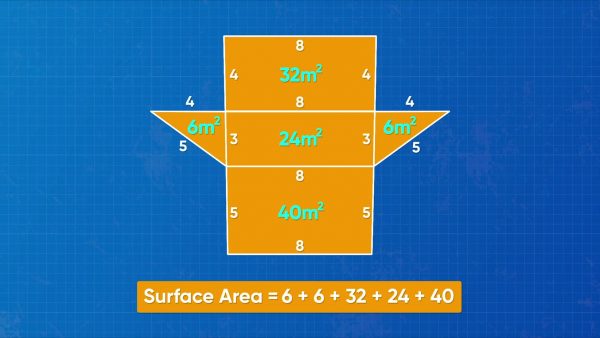
Find the surface area of a skateboard ramp. You are building a skateboard ramp out of wood. You need to know the surface area of the ramp to purchase enough wood to cover it. The ramp is a triangular prism. There are two right triangular faces and three rectangular faces. The triangle sides have base 3 meters and height 4 meters. So the area of each triangle side is [ggfrac]1/2[/ggfrac](3)(4) = 6 square meters. The ramp is 8 meters wide, so there are three rectangular sides, 3 × 8, 4 × 8 and 5 × 8. They have areas 24, 32, and 40 square meters. To find the surface area, add up all of these areas: 6+6+24+32+40=108 square meters. That means the ramp uses 108 square meters of wood. Try this one yourself: The two right triangles on a triangular prism have side lengths 5 meters, 12 meters, and 13 meters. The length across the prism is 4 meters. What is the surface area, in square meters, of the prism?

Determine a 3D shape from its net. What 3D shape can have a net with 2 right triangles and 3 rectangular faces? It’s a triangular prism! How is the 3D shape different if the net has 2 pentagons and 5 rectangles? Now we have a pentagonal prism. The shapes on the net of a rectangular prism are predictable in a different way: all 6 of its faces are rectangles, like when a cardboard box is completely unfolded. Another important comparison involves prisms and pyramids. Can you tell the difference between a triangular prism and a square pyramid just by looking at a net? Both of these nets have 5 shapes, and they both contain triangles. However, the biggest difference is that the square pyramid has 4 triangles, while the triangular prism has 2. Try this one yourself: What 3D shape has a net with exactly 6 rectangles and 2 hexagons?

Many careers use surface area. Engineers use surface area when they build tools that go up in space. Satellites, and many other instruments, are covered in insulating foil. This foil protects them from the extreme cold in space. Engineers use surface area to know how much foil they need for each part of their build. Chemists are another kind of scientists who use surface area. Chemists study matter, and they need to understand surface area because it affects how quickly chemicals react. For example, when something is ground up into a powder, its surface area increases, which speeds up a chemical reaction. A different kind of career where surface area is important is graphic design. Suppose a graphic designer is making a label for a soup can, and the label needs to wrap perfectly around the can. The designer must change the size of the label to work well with the surface area of the can.