
Students learn to find all factor pairs for a whole number in the range 1-100. Students will also recognize that a whole number is a multiple of each of its factors. They will determine whether a given whole number in the range 1-100 is a multiple of a given one-digit number and whether a given whole number in the range 1-100 is prime or composite.
To better understand 2-step algebraic equations…
LET’S BREAK IT DOWN!
Solve equations with addition and multiplication.
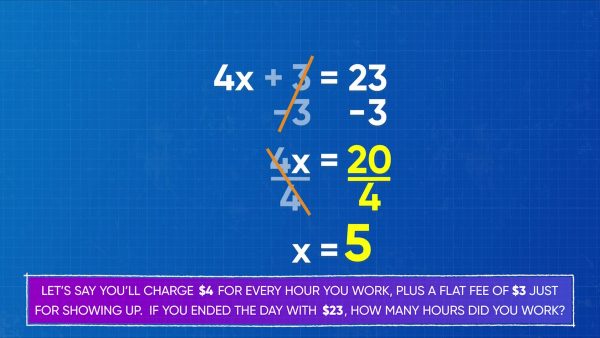
To rake leaves for your neighbors, you charge $4 for every hour you work, plus a flat fee of $3 for showing up. If you raked one lawn for $23, how many hours did you work? We can represent this using an equation, if we let x be the number of hours worked. We write 4x + 3 = 23. To get x on its own, we need to get rid of everything else on the left side. We can do that by using inverse operations. The inverse of + 3 is – 3, so we subtract 3 on both sides. Then we have 4x = 20. Next, 4x means 4 times x, and the inverse is to divide by 4. So we divide both sides by 4, and then we have x = 5. You worked for 5 hours! Now you try: Find x if 3x + 5 = 17.
How can we check our work?

We solved 4x + 3 = 23, and found that x = 5. If we want to check our answer, we can do that by substituting the answer into the original equation. Now that we know that x = 5, we can substitute 5 for x in the equation, so that we get 4(5) + 3 = 23. 4 times 5 is 20, and adding 3 to that is 23. Since both sides of the equal sign have the same value, we know that our work checks out! Now you try: Check if x = 2 is true for 6x + 4 = 16.
Solve equations with multiplication and subtraction.

You got a deal at the local record store. You bought 5 records and got $7 off. If your total came to $98, how much was each record, assuming they all cost the same amount? If we let x be the price of a record, our equation becomes 5x – 7 = 98. First we want to get rid of – 7, and the inverse operation to subtraction is addition. So, we add 7 on both sides. Now we have 5x = 105. If we want to have only one x on the left side, we can divide both sides by 5. We get x = 21. So, each record cost $21! Now you try. Find x if 3x – 7 = 29.
Solve two-step equations with fractions.

You took out one third of the money in your piggy bank, and you already have $8 in your pocket. If the total amount of money you have now is $16, how much was in the piggy bank? If we let x be the amount of money in the piggy bank, then our equation is [ggfrac]x/3[/ggfrac]+8=16. Remember that the line between x and 3 means division. To solve for x, first we subtract 8 from both sides, and now we have [ggfrac]x/3[/ggfrac]=8. Since x is divided by 3, the inverse operation is multiplication, so we multiply both sides by 3 to get x alone. Now we have x=24. That means that originally you had $24 in the piggy bank! Now you try: Find x if [ggfrac]x/5[/ggfrac]+2=22.
WHAT ARE 2-STEP ALGEBRAIC EQUATIONS VOCABULARY
WHAT ARE 2-STEP ALGEBRAIC EQUATIONS DISCUSSION QUESTIONS
What are the operations in the equation 4x – 5 = 7? What operations do you need to use to solve for x?
To solve 4x – 5 = 7, should you divide first or add first?
How can you solve x3-2=2?
What are two different ways you can solve 2(x – 3) = 8?
To solve 2x + 3 = 5, Sylvia first subtracted 5 from both sides. What did she do wrong?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial





