
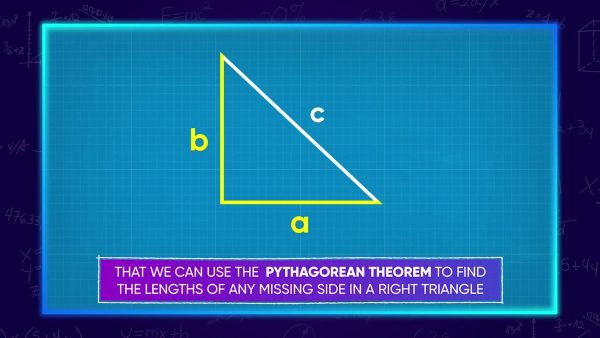
The Pythagorean Theorem is a formula that relates the lengths of the legs and the length of the hypotenuse in a right triangle. The formula is a2+b2=c2. You can use the formula to find a missing side length. You can also use the formula to see if a given set of side lengths could form a right triangle.
To better understand the Pythagorean Theorem…
LET’S BREAK IT DOWN!
Birthday Party
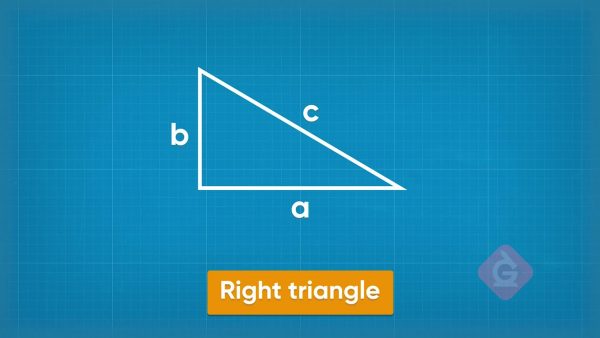
The Pythagorean Theorem is a formula that shows how the side lengths of a right triangle are related. The shorter two sides of the triangle are called legs. One leg has length a and the other leg has length b. The longest side is called the hypotenuse. It has length c. The formula is a2+b2=c2. Find the length of c if a = 3 and b = 4. 32 + 42 = 9 + 16 = 25. So, c2 = 25. That means c = 5. Try this one yourself: For a right triangle, find the length of the hypotenuse if a=5 and b=12.
Skateboard Ramp

The bottom of a skateboard ramp is 100 centimeters long. The height of the ramp is 30 centimeters. What is the length of the ramp part? Substitute 30 and 100 into the formula and find the value of c. 302 + 1002 = 900 + 10,000 = 10,900. Take the square root of 10,900 to find the value of c. The result is irrational, so round to give an approximate answer. c ≈ 104.4 centimeters. The ramp part of the skateboard ramp is approximately 104.4 centimeters long. Try this one yourself: For a right triangle, find the length of the hypotenuse if the base is 6 m and the height is 7 m. Use a calculator, and round your answer to the nearest tenth.
Dog Ramp
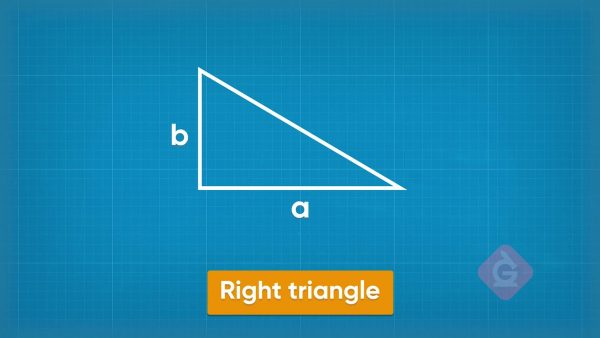
The design for a dog ramp says that the longest side is 5 feet long and the base is 4 feet long. What is the height of the ramp? Substitute those two lengths into the formula. You can substitute 4 for either a or b. a2+42=52, so a2+16=25. Subtract 16 from both sides to isolate the a2. a2=9. Since 3×3=9, a=3. The height of the dog ramp is 3 feet. Try this one yourself: One leg of a right triangle is 6 feet long. The hypotenuse is 10 feet long. What is the length of the other side?
Beehouse
If you have a right triangle, then the side lengths make this equation true: a2+b2=c2. Another mathematical fact is that, if a2+b2=c2, then the triangle is a right triangle. For example, three pieces of wood are cut to lengths of 8 centimeters, 15 centimeters, and 17 centimeters. Can these three lengths fit together to make a bee house in the shape of a right triangle? The longest side is 17, so set c=17. Set a=8 and b=15 for the legs. Squaring these numbers, we get a2=64, b2=225, and c2=289. Then, the sum 64+225 is 289. Since a2+b2 has the same value as c2, that means the three pieces of wood can form a right triangle. Try this one yourself: Can the lengths 7 centimeters, 24 centimeters, and 25 centimeters form a right triangle?
PYTHAGOREAN THEOREM VOCABULARY
PYTHAGOREAN THEOREM DISCUSSION QUESTIONS
When can you use the Pythagorean Theorem?
How is squaring, as in a2, different from doubling, as in 2a?
How would you find the length of the longest side of a triangle if the shorter two sides measure 6 units and 8 units?
How would your calculations change if one leg measures 6 units and the hypotenuse measures 8 units?
How can the Pythagorean Theorem help you find a distance on the coordinate plane?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial
We use cookies to make your experience with this site better. By using this site you agree to our use of cookies. Click "Decline" to delete and block any non-essential cookies for this site on this specific property, device, and browser. Please read our privacy policy for more information on the cookies we use.Learn More
We use cookies to improve your experience. By using this site, you agree to our use of cookies. Click "Decline" to block non-essential cookies. See our privacy policy for details.Learn More





