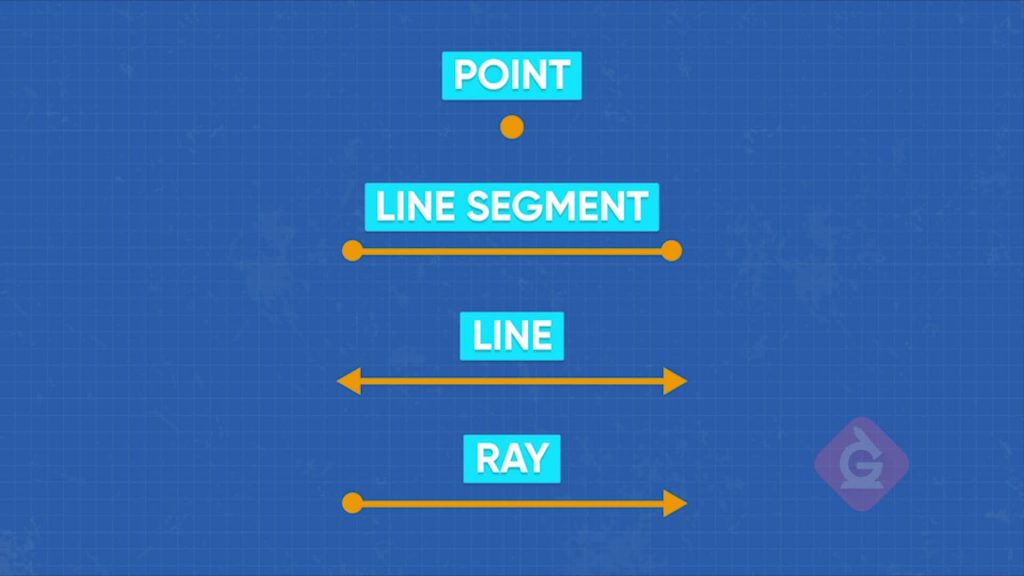
Lines, line segments, and rays are mathematical objects that you can see in the world around you. Lines are straight and go on forever in either direction, while line segments have a start and end point. Ray have a start point but go on straight forever in the other direction.
To better understand lines, line segments, and rays…
LET’S BREAK IT DOWN!
Skyscraper Blueprint

A blueprint of a skyscraper has points in many places. The outer edge of the building has a point wherever there is a corner. These corners are locations where two parts of the building meet, but they don’t have their own length or width. You can imagine that the exact place where one of these points is located looks like a small dot. When an object starts from a point and goes on forever in one direction, that’s called a ray. Think of a ray like one from the sun: light starts at the sun then goes on forever in one direction. When an object starts from one point and then ends at another point, like the height of a building, that’s called a line segment. It’s a portion of a line, which would go on forever in two directions. Try this one yourself: Draw a simple figure of a house or building. Exchange papers with another student. In a new color, draw a point wherever you see two lines or curves meet. Exchange papers again to see if any points were missed.
The Game Show

A point tells you exactly where something is located. For example, a map of the state of Illinois may show a point for the city of Chicago. A ray goes off forever in one direction from a single starting point. Imagine a laser being shined into space! Line segments have a start and an end. If a window is covered with horizontal blinds, each one of the blinds is like a line segment. Lines go on forever in two directions. The horizon is like a line. It seems to be straight and goes off beyond our sight to the left and to the right. Try this one for yourself: Draw a map of your classroom. Include line segments as the border of the room and points as the locations of important objects. Do you see any rays or lines? Explain whether you do or do not.
Train Tracks

Straight train tracks are always the same distance apart. Since they seem to go on forever, you can think of them as parallel lines. Skiing is an activity where parallel lines are important as well. If you keep your skis parallel, you have a better chance of not falling, so imagine parallel lines drawn over your two skis when you’re trying to keep your balance. In contrast, some objects not only cross each other but do so in a very precise way. For example, a suspension bridge can have two metal wires that meet at a point and form a 90-degree angle. These wires are described as perpendicular. They make a “square corner,” also known as a right angle. Street intersections often meet at a right angle. In fact, they make four different right angles: one on each side of each street. A ladder has both parallel and perpendicular line segments: the steps of the ladder are parallel to each other, while the sides of the ladder are perpendicular to the steps. Try this one for yourself: Find pictures of real-life objects that have parallel and perpendicular parts in them. Explain why you think it is important for the parts to be parallel or perpendicular.
Comparing Lines

Parallel lines and line segments are always the same distance apart, like the markings on a football field. You can look at sections of railroad tracks and see that the tracks are always the same distance apart. The tracks made by skis can also form parallel lines. Perpendicular line segments form a right angle, like where the walls and floor meet on a blueprint drawing. Perpendicular lines may be drawn on a grid, showing how far left/right and up/down a point is from the center of the grid. Try this one yourself: Create a piece of artwork that contains parallel line segments and perpendicular line segments. Use one color to highlight or darken the parallel segments, and another color to show off the perpendicular segments.
Classifying Shapes

A rectangle has 2 sets of perpendicular sides. They make 4 right angles. Rectangles also have 2 sets of parallel sides. On the other hand, triangles never have parallel sides because there are only 3 sides and they all need to connect. Triangles can have 2 perpendicular sides. Regular hexagons, the kinds that have all equal angles and all equal sides, have 3 sets of parallel sides and no perpendicular sides. Trapezoids always have one pair of parallel sides. Try this one yourself: Look up the definition of a trapezoid in several different sources, such as online math dictionaries and textbook glossaries. Do all of the definitions of a trapezoid agree with each other, or can you find an important difference among the definitions?
LINES, LINE SEGMENTS, & RAYS VOCABULARY
LINES, LINE SEGMENTS, & RAYS DISCUSSION QUESTIONS
You use the word "line" in your daily life and in math. How are the ways you use the word different?
Are the sides of a shape made from lines or line segments?
Where in this room do you see shapes with parallel or perpendicular sides?
What shapes have parallel sides? What shapes have perpendicular sides?
Can rays form angles? What about lines?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial





