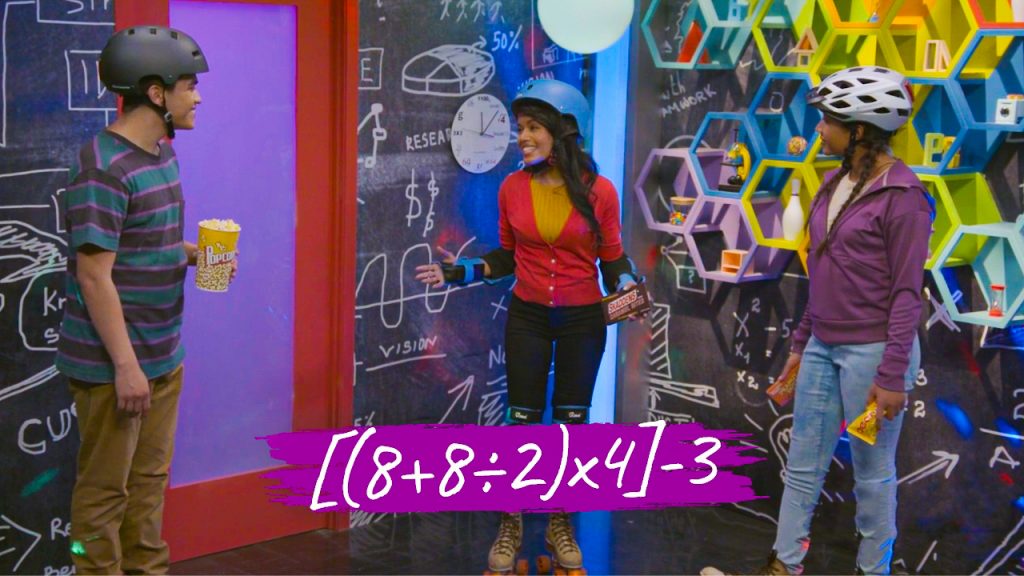
When an expression has two or more operations, the order those operations are evaluated is important. Order of operations is a set of rules for deciding how operations are evaluated in an expression.
To better understand the order of operations…
LET’S BREAK IT DOWN!
Pull Up Exercise Program

An expression is a math phrase that does not include an equal sign, like 4 + 5 or 6 x 5 x 3. You can write expressions to represent real-world situations to make finding the answer easier. Suppose your exercise program for the week is to do 8 pull ups on the first day and then to do 4 pull ups every day for 3 days. You can write the expression 8 + 4 x 3 to represent the total number of pull ups you need to do. To find the correct answer, you need to evaluate the operations in the correct order. First, you do all of the multiplication and division, from left to right. The expression 8 + 4 x 3 has multiplication. 8 + 4 x 3 = 8 + 12. Then, you do all of the addition or subtraction, from left to right. 8 + 12 = 20. You need to do 20 pull ups in all. Try this one yourself: Suppose your friend does 3 pull ups the first day and then 5 pull ups a day for the next 10 days. Write an expression to represent the number of pullups in all your friend will do, then evaluate the expression.
Bicep and Tricep Exercise Program

You can use parentheses "()" to help indicate the order in which operations should be evaluated. Any operations inside parentheses must be done first. To get fit for your pull up program you need to do 6 bicep exercises and 2 triceps exercises 4 times a day. The expression 6 + 2 x 4 shows all the correct numbers and operations needed to calculate the total number of exercises, but the operations will not be calculated in the right order to get the answer. You need to first find the sum of 6 and 2 before multiplying by 4. When written without parentheses, order of operations says that in the expression 6 + 2 x 4 you need to multiply first, then add. The expression (6 + 2) x 4 represents the problem by showing that the addition happens first. Find the total number of exercises by first finding 6 + 2 = 8. Then multiply 8 x 4 = 32. You will do 32 exercises in all each day. Try this one yourself: Suppose your friend does 4 bicep and 4 triceps exercises 3 times a day. Write an expression to represent the number of exercises your friend will do in one day, then evaluate the expression.
Buying Model Cars with Dollars

Let’s say you and your 3 friends are collectors of model cars. The red model car usually costs 8 dollars, but is on sale for 3 dollars off. The black model car costs 7 dollars. You want to buy a red car and a black car for each of your 3 friends. How much will this cost? You can write the expression in parts. First, find the cost of one red card: 8 – 3. Then, the cost of a black card: 7. Add to find the cost of one red and one black cars together: (8 – 3) + 7. Then multiply by 3 to find the cost of 3 sets: 3 x [(8 – 3) + 7]. Notice that we had to use something besides parentheses to show a new level of grouping. Now let's solve it. The subtraction is inside parenthesis, so it needs to be done first: 3 x [5 + 7]. The addition is inside brackets, so it needs to be done next: 3 x 12. Now that all brackets and parenthesis are gone, we do the multiplication: 36. It will cost you 36 dollars to buy a red car and a black car for each of your 3 friends. Try this one yourself: Suppose you want to buy 2 red cars and 5 black cars for both of your two friends. How much will that cost? Write an expression to represent the cost of the cars, then evaluate the expression.
Game Show
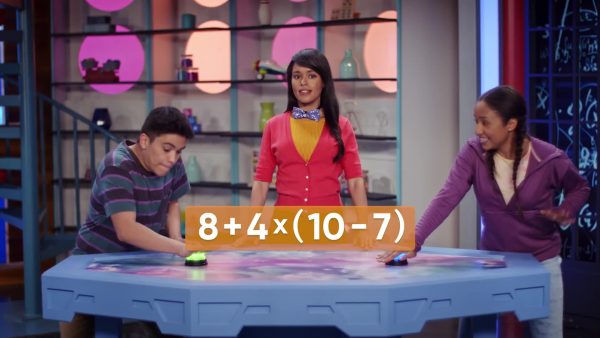
You are on a game show and you need to evaluate this expression. How can you evaluate [(8 + 8 ÷ 2) x 4] -3? First, notice that there are brackets and parentheses. You need to start with the expression inside the parenthesis, 8 + 8 ÷ 2. Let’s look at that separately. This expression has addition and division. Order of operations says to do the division first: 8 + 4. Then you can add: 8 + 4 = 12. Now the expression looks like this: [12 x 4] – 3. Next evaluate the expression inside the brackets. 12 x 4 = 48. Now the expression is 48 – 3. Subtract to find the final answer. 48 – 3 = 45. The answer is 45. Try this one yourself: [(5 + 6 ÷ 2) x 2] - 7 and show how you evaluate this expression.
ORDER OF OPERATIONS VOCABULARY
Work within parentheses first.
Then do multiplication working from left to right.
Then do addition and subtraction working from left to right.
ORDER OF OPERATIONS DISCUSSION QUESTIONS
Do you get the same value when you evaluate (5 – 2) – 1 and 5 – (2 – 1)? Explain.
Describe the steps you would take to evaluate this expression: [(6 + 2) – 3] x 8
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial





