Equivalent expressions are expressions have the same value. You can use the rules of integer exponents to write expressions with exponents in simpler ways.
To better understand integer exponents…
LET’S BREAK IT DOWN!
Exponents represent repeated multiplication.
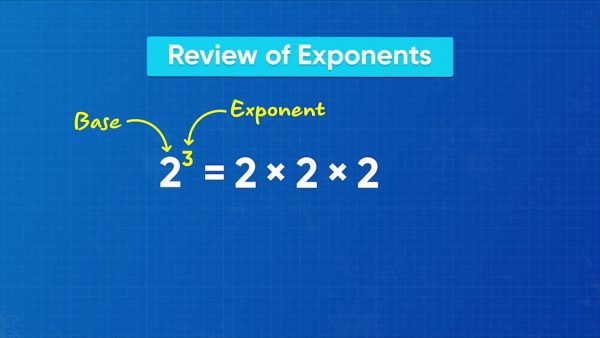
An exponential expression has a base and a power. In 23, 2 is the base and 3 is the power. The base tells you the number that is multiplied. The power tells you how many times to multiply the base. So, 23 = 2 × 2 × 2. Similarly, 34 = 3 × 3 × 3 × 3. Now you try: Rewrite 25as a multiplication expression.
Negative exponents represent fractions.
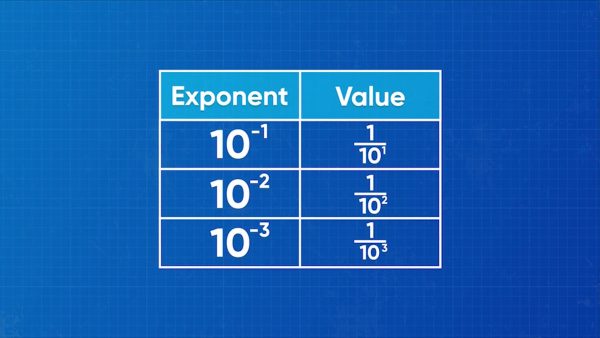
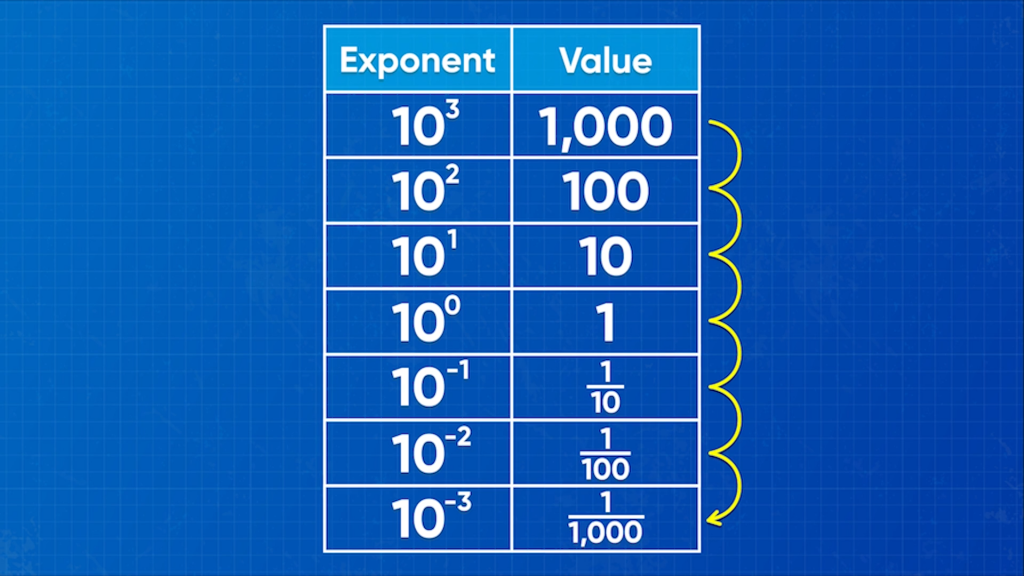
Consider the following equations. 103 = 10 × 10 × 10. 102 = 10 × 10. 102 is ten times less than 103. 101 = 10. 101 is ten times less than 102. 100 = 1, which is ten times less than 101. To continue this pattern, 10–1 must be ten times less than 1, which is [ggfrac]1/10[/ggfrac]. 10–2 =[ggfrac] 1/10 × 10[/ggfrac], which is [ggfrac]1/100[/ggfrac]. 10–3 = [ggfrac]1/10× 10× 10[/ggfrac], which is [ggfrac]1/1,000[/ggfrac]. An exponent with a negative power represents 1 over the same exponent with a positive power. 10–2 = [ggfrac]1/102[/ggfrac]. This works for all negative exponents, such as 2–6 = [ggfrac]1/26[/ggfrac]. Now you try: Rewrite 3–4 as an exponent with a positive power.
Use negative exponents to find the length of an amoeba.
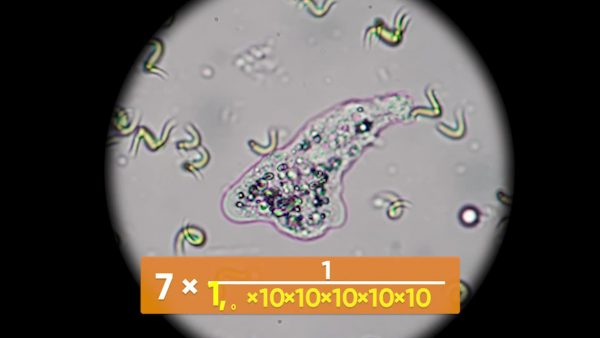
An amoeba has length 7 × 10–6 m. First, evaluate the exponent: 10–6 = [ggfrac]1/106[/ggfrac] = [ggfrac]1/1,000,000[/ggfrac]. That's one millionth. 7 × one millionth is 7 millionths. The amoeba is 7 millionths of a meter long.
Multiply and divide exponential expressions with integer exponents.
Many careers use negative exponents.

Here are three examples from many careers that use negative exponents. Microbiologists use negative exponents to represent the size of very small organisms, like bacteria. Veterinarians can represent the weight of very light animals using negative exponents. Chemists use negative exponents to represent the weights of elements and compounds.
INTEGER EXPONENTS VOCABULARY
INTEGER EXPONENTS DISCUSSION QUESTIONS
What is the relationship between the following expressions: 23, 22, 21, 20, 2–1, 2-2
What is the rule to rewrite an exponential expression with a negative power as a rational number?
An atom weighs 2 × 10–23 grams. How can you write that as an exponential expression with a positive exponent?
How does the product of powers rule change when one or more powers are negative?
How does the quotient of powers rule change when one or more powers are negative?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial





