Two fractions have unlike denominators if the numbers in the denominators are not the same. You can use multiplication and division to rewrite fractions to have a common denominator.
To better understand adding and subtracting fractions with unlike denominators…
LET’S BREAK IT DOWN!
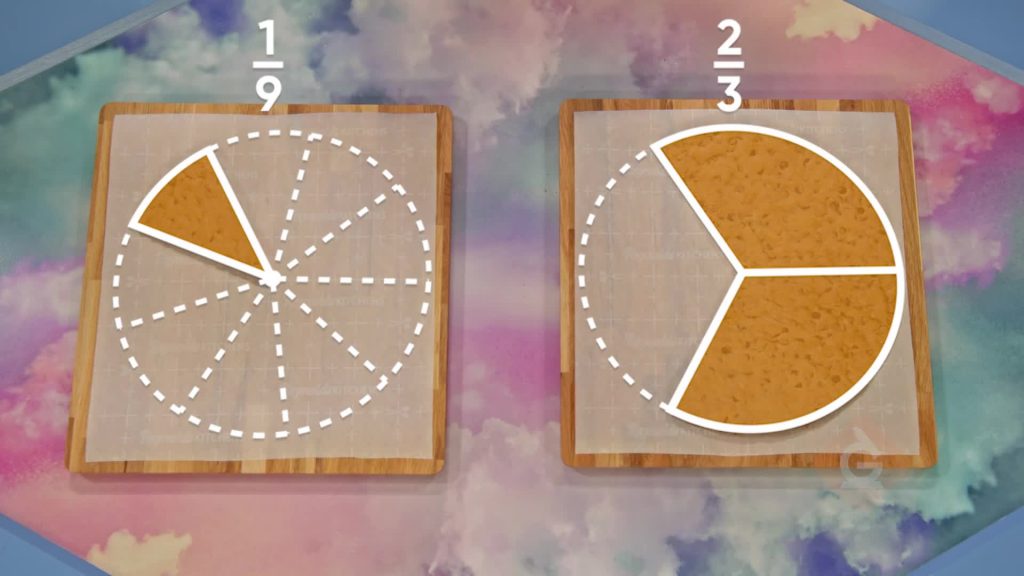
Cookies

Let's say that Marcos and April each have a large cookie. They each ate part of their cookie. Marcos has [ggfrac]1/9[/ggfrac] of his cookie left and April has [ggfrac]2/3[/ggfrac] of hers left. How much cookie do they have left, combined? To answer this question, you need to rewrite the fractions with a common denominator by finding equivalent fractions, and then add. Start with the fraction with the smaller denominator, [ggfrac]2/3[/ggfrac]. We can find an equivalent fraction by multiplying both the numerator and denominator by the same number. Multiply [ggfrac]2/3[/ggfrac] by [ggfrac]3/3[/ggfrac] to find an equivalent fraction with denominator 9. [ggfrac]2/3[/ggfrac] x [ggfrac]3/3[/ggfrac] = [ggfrac]6/9[/ggfrac].[ggfrac]6/9[/ggfrac] has the same denominator as [ggfrac]1/9[/ggfrac] and is equivalent to [ggfrac]2/3[/ggfrac]. Now we can rewrite the original addition as [ggfrac]1/9[/ggfrac] + [ggfrac]6/9[/ggfrac] = [ggfrac]7/9[/ggfrac]. They have [ggfrac]7/9[/ggfrac] of a cookie left. Try this one yourself. You ate [ggfrac]2/5[/ggfrac] of a pizza and your sister ate [ggfrac]1/10[/ggfrac] of the same pizza. How much of the pizza did you eat in all?
Algorithm for Finding a Common Denominator

Let's say you want to add [ggfrac]1/3[/ggfrac] + [ggfrac]2/5[/ggfrac]. You know that you need to find a common denominator. Starting with [ggfrac]1/3[/ggfrac], list equivalent fractions: [ggfrac]1/3[/ggfrac] x [ggfrac]2/2[/ggfrac] = [ggfrac]2/6[/ggfrac], [ggfrac]1/3[/ggfrac] x [ggfrac]3/3[/ggfrac] = [ggfrac]3/9[/ggfrac], [ggfrac]1/3[/ggfrac] x [ggfrac]4/4[/ggfrac] = [ggfrac]4/12[/ggfrac], [ggfrac]1/3[/ggfrac] x [ggfrac]5/5[/ggfrac] = [ggfrac]5/15[/ggfrac], and [ggfrac]1/3[/ggfrac] x [ggfrac]6/6[/ggfrac] = [ggfrac]6/18[/ggfrac]. None of those fractions have a denominator of 5, so you need to find equivalent fractions for [ggfrac]2/5[/ggfrac] as well: [ggfrac]2/5[/ggfrac] x [ggfrac]2/2[/ggfrac] = [ggfrac]4/10[/ggfrac], [ggfrac]2/5[/ggfrac] x [ggfrac]3/3[/ggfrac] = [ggfrac]6/15[/ggfrac], and [ggfrac]2/5[/ggfrac] x [ggfrac]4/4[/ggfrac] = [ggfrac]8/20[/ggfrac]. Both [ggfrac]1/3[/ggfrac] and [ggfrac]2/5[/ggfrac] have an equivalent fraction with a denominator of 15. Rewrite the original addition as [ggfrac]5/15[/ggfrac] + [ggfrac]6/15[/ggfrac] = [ggfrac]11/15[/ggfrac].
There is a faster way to find a common denominator. If you multiply the numerator and the denominator of each fraction by the denominator of the other fraction, you always get fractions with a common denominator. Here's how this works: Starting with [ggfrac]1/3[/ggfrac], you see that the other fraction, [ggfrac]2/5[/ggfrac], has a denominator of 5 so you multiply the numerator and denominator by 5: [ggfrac]1/3[/ggfrac] x [ggfrac]5/5[/ggfrac] = [ggfrac]5/15[/ggfrac]. Next, you see that [ggfrac]1/3[/ggfrac] has a denominator of 3, so you multiply the numerator and denominator of the other fraction by 3: [ggfrac]2/5[/ggfrac] x [ggfrac]3/3[/ggfrac] = [ggfrac]6/15[/ggfrac]. Rewrite the original addition as [ggfrac]5/15[/ggfrac] + [ggfrac]6/15[/ggfrac] = [ggfrac]11/15[/ggfrac]. Try this one yourself. Add [ggfrac]1/6[/ggfrac] + [ggfrac]3/4[/ggfrac] by finding a common denominator using the faster way.
Guinea Pig Weights

Let's say that you have two tiny guinea pigs. One weighs [ggfrac]4/5[/ggfrac] of a pound and the other weighs [ggfrac]2/3[/ggfrac] of a pound. You want to figure out how much more one guinea pig weighs than the other. You can find this difference using the equation [ggfrac]4/5[/ggfrac] - [ggfrac]2/3[/ggfrac] = ?. First, find the equivalent fractions that have a common denominator. The second fraction has a denominator of 3, so multiply the numerator and denominator of the first fraction by 3. [ggfrac]4/5[/ggfrac] x [ggfrac]3/3[/ggfrac] = [ggfrac]12/15[/ggfrac]. Next, multiply [ggfrac]2/3[/ggfrac] x [ggfrac]5/5[/ggfrac] since 5 is the denominator of [ggfrac]4/5[/ggfrac]. [ggfrac]2/3[/ggfrac] x [ggfrac]5/5[/ggfrac] = [ggfrac]10/15[/ggfrac]. Rewrite the original subtraction [ggfrac]4/5[/ggfrac] - [ggfrac]2/3[/ggfrac] as [ggfrac]12/15[/ggfrac] - [ggfrac]10/15[/ggfrac] = [ggfrac]2/15[/ggfrac]. One guinea pig weighs [ggfrac]2/15[/ggfrac] of a pound more than the other guinea pig. Try this one yourself. My bag of candy weighs [ggfrac]3/4[/ggfrac] of a pound and my friend's bag of candy weighs [ggfrac]2/3[/ggfrac] of a pound. How much more does my bag of candy weigh?
Rollerblading and Long Jumping

Let's say that you rollerbladed 2[ggfrac]3/4[/ggfrac] miles yesterday and 3[ggfrac]1/3[/ggfrac] miles today. How many total miles did you rollerblade? To answer this, solve 2[ggfrac]3/4[/ggfrac] + 3[ggfrac]1/3[/ggfrac]. You can add fractions and whole numbers separately and combine the answers. Let's start with the fractions and add [ggfrac]3/4[/ggfrac] + [ggfrac]1/3[/ggfrac]. They have unlike denominators, so multiply each fraction's numerator and denominator by the other fraction's denominator to get equivalent fractions: [ggfrac]3/4[/ggfrac] x [ggfrac]3/3[/ggfrac] = [ggfrac]9/12[/ggfrac] and [ggfrac]1/3[/ggfrac] x [ggfrac]4/4[/ggfrac] = [ggfrac]4/12[/ggfrac]. Add the new numerators. [ggfrac]9/12[/ggfrac]+ [ggfrac]4/12[/ggfrac] = [ggfrac]13/12[/ggfrac]. Since this fraction is greater than 1, regroup from an improper fraction to a mixed number: [ggfrac]13/12[/ggfrac] = [ggfrac]12/12[/ggfrac] + [ggfrac]1/12[/ggfrac] = 1[ggfrac]1/12[/ggfrac]. Next, add the whole numbers: 2 + 3 = 5. Then combine the totals: 5 + 1[ggfrac]1/12[/ggfrac] = 6[ggfrac]1/12[/ggfrac]. You rollerbladed a total of 6[ggfrac]1/12[/ggfrac] miles.
Let's look at an example of subtracting mixed numbers. Let's say Marcos had a long jump of 5[ggfrac]1/6[/ggfrac] feet and April jumped 4[ggfrac]2/3[/ggfrac] feet. We can figure out how much farther Marcos jumped by solving 5[ggfrac]1/6[/ggfrac] - 4[ggfrac]2/3[/ggfrac] = ?. Start by finding [ggfrac]1/6[/ggfrac] - [ggfrac]2/3[/ggfrac]. The denominators are unlike, so we need to find equivalent fractions with a common denominator: 2 x 3 = 6, so multiply the numerator and denominator of [ggfrac]2/3[/ggfrac] by 2: [ggfrac]2/3[/ggfrac] x [ggfrac]2/2[/ggfrac] = [ggfrac]4/6[/ggfrac]. The fraction subtraction is now [ggfrac]1/6[/ggfrac] - [ggfrac]4/6[/ggfrac]. 4 is greater than 1, so we need to regroup from 5 to make a fraction greater than [ggfrac]4/6[/ggfrac]. Regroup 1 one into 6 sixths. 5 = 4[ggfrac]6/6[/ggfrac]. Add the new sixths to [ggfrac]1/6[/ggfrac]. [ggfrac]6/6[/ggfrac] + [ggfrac]1/6[/ggfrac] = [ggfrac]7/6[/ggfrac]. Now we can subtract the fractions: [ggfrac]7/6[/ggfrac] - [ggfrac]4/6[/ggfrac] = [ggfrac]3/6[/ggfrac]. Finally, subtract the remaining whole number parts of the mixed numbers: 4 - 4 = 0. Marcos jumped [ggfrac]3/6[/ggfrac] of a foot farther than April. Try this one yourself. I hiked 6[ggfrac]1/8[/ggfrac] miles on Saturday and another 4[ggfrac]2/3[/ggfrac] miles on Sunday. How many total miles did I hike this weekend?
ADD AND SUBTRACT FRACTIONS (UNLIKE DENOMINATORS) VOCABULARY
ADD AND SUBTRACT FRACTIONS (UNLIKE DENOMINATORS) DISCUSSION QUESTIONS
Which part of a fraction tells you the number of equal-sized parts that the whole is broken into?
What is the meaning of the numerator when adding or subtracting fractions?
How can we find equivalent fractions with a common denominator for two fractions with unlike denominators?
Which of the following benchmark numbers—0, [ggfrac]1/2[/ggfrac], or 1—can you use to help estimate when adding [ggfrac]4/9[/ggfrac] to another fraction?
Rafay says that 5 - 3[ggfrac]1/3[/ggfrac] = 2[ggfrac]1/3[/ggfrac]. Is Rafay correct? If not, what did Rafay do wrong?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial





